
分析 (1)直接利用配方法求函数的解析式;
(2)把已知函数解析式变形,换元后结合对勾函数的单调性求得函数值域.
解答 解:(1)由g(x+$\frac{1}{x}$)=x2+$\frac{1}{{x}^{2}}$=$(x+\frac{1}{x})^{2}-2$,
得g(x)=x2-2(x≥2或x≤-2);
(2)h(x)=$\frac{4{x}^{2}-12x-3}{2x+1}$=$\frac{(2x+1)^{2}-8(2x+1)+4}{2x+1}$=$(2x+1)+\frac{4}{2x+1}-8$.
∵x∈[0,1],∴2x+1∈[1,3],
令2x+1=t,(t∈[1,3]),
则函数f(t)=t+$\frac{4}{t}-8$在[1,2]上为减函数,在[2,3]上为增函数,
∵f(1)=-3,f(2)=-4,f(3)=-$\frac{11}{3}$.
∴f(t)∈[-4,-3],故函数h(x)的值域为[-4,-3].
点评 本题考查函数解析式的求解及常用方法,考查了对勾函数的性质,训练了利用函数的单调性求函数的值域,是中档题.


科目:高中数学 来源: 题型:解答题
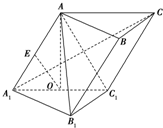 如图,在斜三棱柱ABC-A1B1C1中,点O、E分别是A1C1、AA1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O、E分别是A1C1、AA1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
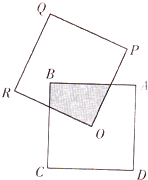 小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$.
小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com