
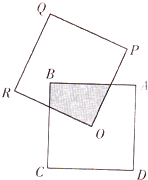
 小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$.
小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$. 分析 连OA,OB,设OR交BC于M,OP交AB于N,由四边形ABCD为正方形,得到OB=OA,∠BOA=90°,∠MBO=∠OAN=45°,而四边形ORQP为正方形,得∠NOM=90°,所以∠MOB=∠NOA,则△OBM≌△OAN,即可得到S四边形MONB=S△AOB,从而求出小明射中阴影部分的概率值.
解答 解:连OA,OB,设OR交BC于M,OP交AB于N,
如图示:
∵四边形ABCD为正方形,
∴OB=OA,∠BOA=90°,∠MBO=∠OAN=45°,
而四边形ORQP为正方形,
∴∠NOM=90°,
∴∠MOB=∠NOA,
∴△OBM≌△OAN,
∴S四边形MONB=S△AOB=$\frac{1}{4}$×2×2=1,
即它们重叠部分的面积为1,
总面积是7,
故小明射中阴影部分的概率P=$\frac{1}{7}$,
故答案为:$\frac{1}{7}$.
点评 本题考查了几何概型问题,考查旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了正方形的性质.


科目:高中数学 来源: 题型:选择题
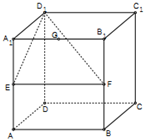 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若p,则q”与命题“若非q,则非p”互为逆否命题 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若f′(x)=0,则x为y=f(x)的极值点”为真命题 | |
| D. | “am2<bm2”是“a<b”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
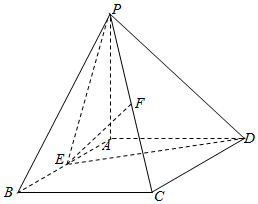 如图,已知四棱锥P-ABCD的底面为矩形,PA=AD=1,AB=2,且PA⊥平面ABCD,E,F分别为AB,PC的中点.
如图,已知四棱锥P-ABCD的底面为矩形,PA=AD=1,AB=2,且PA⊥平面ABCD,E,F分别为AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com