
分析 设公共点(x0,y0),根据题意得到,f(x0)=g(x0),f′(x0)=g′(x0),解出b关于a的函数关系式,然后利用导数研究b关于a的函数的单调性,从而求出b的最大值.
解答 解:(I)设y=f(x)与y=g(x)(x>0)在公共点(x0,y0)处的切线相同.
f′(x)=x+2a,g′(x)=$\frac{3{a}^{2}}{x}$.
由题意知f(x0)=g(x0),f′(x0)=g′(x0)
即$\left\{\begin{array}{l}{\frac{1}{2}{{x}_{0}}^{2}+2a{x}_{0}=3{a}^{2}ln{x}_{0}+b}\\{{x}_{0}+2a=\frac{3{a}^{2}}{{x}_{0}}}\end{array}\right.$,
解得x0=a或x0=-3a(舍去),
b(a)=$\frac{5{a}^{2}}{2}$-3a2lna(a>0)
b'(a)=5a-6alna-3a=2a(1-3lna)
b'(a)>0?$\left\{\begin{array}{l}{a>0}\\{1-3lna>0}\end{array}\right.$?0<a<${e}^{\frac{1}{3}}$
b'(a)<0?$\left\{\begin{array}{l}{a>0}\\{1-3lna<0}\end{array}\right.$?a>${e}^{\frac{1}{3}}$
可见b(a)max=b(${e}^{\frac{1}{3}}$)=$\frac{3}{2}{e}^{\frac{2}{3}}$.
故答案为:$\frac{3}{2}{e}^{\frac{2}{3}}$.
点评 本题主要考查了利用导数研究曲线上某点切线方程和恒成立问题,以及利用导数研究函数的单调性和最值,同时考查了转化的思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
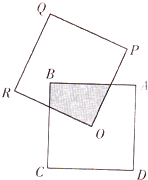 小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$.
小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,+∞) | C. | (-∞,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com