
分析 (1)由已知及正弦定理,两角和的正弦函数公式,三角形内角和定理化简已知可得$cosC=\frac{1}{2}$,结合C的范围,即可得解C的值.
(2)由已知及余弦定理得ab=6,利用三角形面积公式即可计算得解.
解答 (本题满分为12分)
解:(1)由已知及正弦定理得,$cosC(sinAcosB+cosAsinB)=\frac{1}{2}sinC$,
即2cosCsin(A+B)=sinC.
故2cosCsinC=sinC,
可得$cosC=\frac{1}{2}$,
因为:C∈(0,π),
所以$C=\frac{π}{3}$.…(6分)
(2)由已知及余弦定理得,a2+b2-2abcosC=7,
又$a+b=5,C=\frac{π}{3}$,
故a2+b2-ab=(a+b)2-3ab=25-3ab=7,
因此,ab=6,
所以△ABC的面积$S=\frac{1}{2}absinC=\frac{{3\sqrt{3}}}{2}$.…(12分)
点评 本题主要考查了正弦定理,两角和的正弦函数公式,三角形内角和定理,余弦定理,三角形面积公式在解三角形中的综合应用,考查了转化思想,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 样本方差反映了所有样本数据与样本平均值的偏离程度 | |
| B. | 残差平方和越小的模型,拟合的效果越好 | |
| C. | 用相关指数R2来刻画回归效果,R2的值越小,说明模型的拟合效果越好 | |
| D. | 在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是残差平方和 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | $\frac{1}{4}$ | C. | -$\frac{1}{4}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
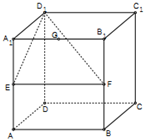 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com