
分析 (1)由题意可知列方程:$\left\{\begin{array}{l}{x=c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,即可求得M(c,$\frac{{b}^{2}}{a}$),由斜率公式可求得a=2c,e=$\frac{c}{a}$=$\frac{1}{2}$;
(2)由(1)可知,椭圆方程为:$\frac{{x}^{2}}{4{c}^{2}}+\frac{{y}^{2}}{{3c}^{2}}=1$,设外接圆的圆心为T(t,0),由丨TA丨=丨TM丨得(t+2c)2+(t-c)2+$\frac{9}{4}$c2,求得T(-$\frac{c}{8}$),求得切线方程,代入椭圆方程,求得丨CD丨,根据点到直线的距离公式及三角形面积公式,代入即可求得c的值,求得椭圆方程.
解答 解:由题意可知:设M(x,y),由$\left\{\begin{array}{l}{x=c}\\{\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1}\end{array}\right.$,
∴M(c,$\frac{{b}^{2}}{a}$),
∴$\frac{\frac{{b}^{2}}{a}}{a+c}$=$\frac{{a}^{2}-{c}^{2}}{a(a+c)}$=$\frac{a-c}{a}$=$\frac{1}{2}$,
∴a=2c,
∴e=$\frac{c}{a}$=$\frac{1}{2}$;
(2)由b2=a2-c2=4c2-c2=3c2,
∴b=$\sqrt{3}$c,
∴椭圆方程为:$\frac{{x}^{2}}{4{c}^{2}}+\frac{{y}^{2}}{{3c}^{2}}=1$,M(c,$\frac{3}{2}$c),A1(-2c,0),
设外接圆的圆心为T(t,0),由丨TA丨=丨TM丨得(t+2c)2=(t-c)2+$\frac{9}{4}$c2,
整理得:6tc=-$\frac{3}{4}$c2,
∴t=-$\frac{c}{8}$,
∴T(-$\frac{c}{8}$,0),
∴kDM=$\frac{\frac{3}{2}c}{c+\frac{c}{8}}$=$\frac{4}{3}$,
∴切线斜率k=-$\frac{3}{4}$,
∴切线方程为y-$\frac{3}{2}$c=-$\frac{3}{4}$(x-c),即3x+4y-9c=0,
代入椭圆方程消y得7x2-18cx+11c2=0,
△=182c2-4×7×11c2=16c2>0,
xD=$\frac{11c}{7}$,yD=$\frac{25c}{14}$,
∴丨CD丨=$\sqrt{({x}_{C}-{x}_{D})^{2}+({y}_{C}-{y}_{D})^{2}}$=$\sqrt{(\frac{11c}{7}-c)^{2}+(\frac{15c}{14}-\frac{3c}{2})^{2}}$=$\frac{5c}{7}$,
F2点到CD的距离d=$\frac{丨3c-9c丨}{5}$=$\frac{6c}{5}$,
由S=$\frac{1}{2}$丨CD丨•d,得$\frac{12}{7}$=$\frac{1}{2}$×$\frac{5c}{7}$×$\frac{6c}{5}$=$\frac{3}{7}{c}^{2}$,
∴c2=4,
∴椭圆方程为$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{12}$=1.
点评 本题考查椭圆的标准方程及简单性质,直线与椭圆的位置关系,点到直线的距离公式及三角形面积公式,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
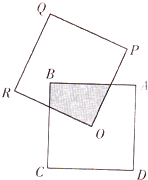 小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$.
小明爱好玩飞镖,现有图形构成如图所示的两个边长为2的正方形ABCD和OPQR,如果O点正好是正方形ABCD的中心,而正方形OPQR可以绕点O旋转,则小明射中阴影部分的概率是$\frac{1}{7}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 1 | D. | -$\frac{1}{2}$或1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com