
分析 (Ⅰ)m=0时,求出函数的导数,解关于导函数的不等式,求出函数的单调区间即可;
(Ⅱ)问题整理得$\frac{lnx-x+1}{x}$<m<$\frac{lnx}{x}$,令g(x)=$\frac{lnx-x+1}{x}$,令h(x)=$\frac{lnx}{x}$,根据函数的单调性求出m的范围即可;
(Ⅲ)根据基本不等式的解法即可证明不等式.
解答 解:(I)当m=0时,f(x)=xlnx,x>0,得f′(x)=lnx+1,
由lnx+1>0,解得x>$\frac{1}{e}$,即f(x)在($\frac{1}{e}$,+∞)上单调递增;
由lnx+1<0,解得0<x<$\frac{1}{e}$,即f(x)在(0,$\frac{1}{e}$)上单调递减.
∴综上,f(x)的单调递增区间为($\frac{1}{e}$,+∞),单调递减区间为(0,$\frac{1}{e}$).…(3分)
(II)已知x∈[$\sqrt{e}$,e2],于是$\frac{{x}^{2}-x}{f(x)}$>1变形为$\frac{x-1}{lnx-mx}$>1,
从而$\frac{1}{lnx-mx}$>$\frac{1}{x-1}$,即0<lnx-mx<x-1,
整理得$\frac{lnx-x+1}{x}$<m<$\frac{lnx}{x}$…(5分)
令g(x)=$\frac{lnx-x+1}{x}$,则g′(x)=$\frac{-lnx}{{x}^{2}}$<0,即g(x)在[$\sqrt{e}$,e2]上是减函数,
∴g(x)max=g($\sqrt{e}$)=$\frac{3\sqrt{e}}{2e}$-1,
令h(x)=$\frac{lnx}{x}$,则h′(x)=$\frac{1-lnx}{{x}^{2}}$,
当$\sqrt{e}$<x<e时,h′(x)>0,即此时h(x)单调递增;
当e<x<e2时,h′(x)<0,即此时h(x)单调递减,
而h($\sqrt{e}$)=$\frac{1}{2\sqrt{e}}$>h(e2)=$\frac{2}{{e}^{2}}$,
∴h(x)min=$\frac{2}{{e}^{2}}$
∴$\frac{3\sqrt{e}}{2e}$-1<m<$\frac{2}{{e}^{2}}$…(9分)
(III)由(I)知当m=0时,f(x)=xlnx在($\frac{1}{e}$,+∞)上是增函数,
∵$\frac{1}{e}$<x1<x1+x2<1,
∴f(x1+x2)=(x1+x2)ln(x1+x2)>f(x1)=x1lnx1,
即lnx1<$\frac{{{x}_{1}+x}_{2}}{{x}_{1}}$ln(x1+x2),同理lnx2<$\frac{{{x}_{1}+x}_{2}}{{x}_{2}}$ln(x1+x2),
所以lnx1+lnx2<($\frac{{{x}_{1}+x}_{2}}{{x}_{1}}$+$\frac{{{x}_{1}+x}_{2}}{{x}_{2}}$)ln(x1+x2)=(2+$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$)ln(x1+x2),
又因为)2+$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$≥4,当且仅当x1=x2时,取等号.
又x1,x2∈($\frac{1}{e}$,1),x1+x2<1,ln(x1+x2),
∴(2+$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$)ln(x1+x2)≤4,
∴lnx1+lnx2<4ln(x1+x2),
∴x1x2<(x1+x2)4.…(14分)
点评 本题主要考查导数的综合应用,要求熟练掌握导数的几何意义,综合性较强,运算量较大.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
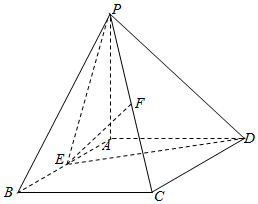 如图,已知四棱锥P-ABCD的底面为矩形,PA=AD=1,AB=2,且PA⊥平面ABCD,E,F分别为AB,PC的中点.
如图,已知四棱锥P-ABCD的底面为矩形,PA=AD=1,AB=2,且PA⊥平面ABCD,E,F分别为AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
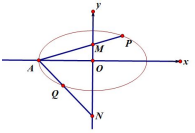 在平面直角坐标系 xOy 中,离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,且A到右准线的距离为6,点P、Q是椭圆C上的两个动点.
在平面直角坐标系 xOy 中,离心率为$\frac{1}{2}$的椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左顶点为A,且A到右准线的距离为6,点P、Q是椭圆C上的两个动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{1}{4}$ | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com