
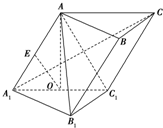
 如图,在斜三棱柱ABC-A1B1C1中,点O、E分别是A1C1、AA1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O、E分别是A1C1、AA1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.分析 (1)由中位线定理得出OE∥AC1,故而OE∥平面AB1C1;
(2)通过证明A1C⊥平面AB1C1得出AB1⊥A1C;
(3)利用V${\;}_{A-{A}_{1}{B}_{1}{C}_{1}}$=V${\;}_{{C}_{1}-A{A}_{1}{B}_{1}}$得出C1到平面AA1B1的距离d,即可得出线面角的正弦值.
解答 证明:(1)∵点O、E分别是A1C1、AA1的中点,
∴OE∥AC1,
又∵EO?平面AB1C1,AC1?平面AB1C1,
∴OE∥平面AB1C1,
(2)∵AO⊥平面A1B1C1,B1C1?平面A1B1C1,
∴AO⊥B1C1,
又∵A1C1⊥B1C1,A1C1∩AO=O,
∴B1C1⊥平面A1C1CA,又A1C?平面A1C1CA,
∴A1C⊥B1C1.
∵AA1=AC,∴四边形A1C1CA为棱形,
∴A1C⊥AC1,又B1C1∩AC1=C1,B1C1?平面AB1C1,AC1?平面AB1C1,
∴A1C⊥平面AB1C1,又AB1?平面AB1C1,
∴AB1⊥A1C.
(3)∵∠BCA=90°,AA1=AC=BC=2,
∴A1O=$\frac{1}{2}$A1C1=1,AC1=2,
∴AO=$\sqrt{A{{A}_{1}}^{2}-{A}_{1}{O}^{2}}$=$\sqrt{3}$,A1B1=$\sqrt{{A}_{1}{{C}_{1}}^{2}+{B}_{1}{{C}_{1}}^{2}}$=2$\sqrt{2}$,AB1=$\sqrt{A{{C}_{1}}^{2}+{B}_{1}{{C}_{1}}^{2}}$=2$\sqrt{2}$,
∴S${\;}_{△{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{2}×2×2$=2,S${\;}_{△A{A}_{1}{B}_{1}}$=$\frac{1}{2}×2×\sqrt{(2\sqrt{2})^{2}-(\frac{2}{2})^{2}}$=$\sqrt{7}$,
∴V${\;}_{A-{A}_{1}{B}_{1}{C}_{1}}$=$\frac{1}{3}{S}_{△{A}_{1}{B}_{1}{C}_{1}}•AO$=$\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{3}$=$\frac{2\sqrt{3}}{3}$.
设点C1到平面AA1B1的距离为d,则V${\;}_{A-{A}_{1}{B}_{1}{C}_{1}}$=V${\;}_{{C}_{1}-A{A}_{1}{B}_{1}}$=$\frac{1}{3}$S${\;}_{△A{A}_{1}{B}_{1}}$•d.
∴$\frac{2\sqrt{3}}{3}$=$\frac{1}{3}×\sqrt{7}×d$,即d=$\frac{2\sqrt{21}}{7}$,
∴A1C1与平面AA1B1所成角的正弦值为$\frac{d}{{A}_{1}{C}_{1}}$=$\frac{{\sqrt{21}}}{7}$.
点评 本题考查了线面平行的判定,线面垂直的判定,空间距离的计算,属于中档题.


 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
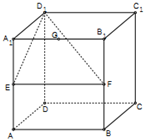 如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,E,F,G分别为棱AA1,BB1,A1B1的中点,则点G到平面EFD1的距离为( )| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{5}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 政治分数x | 89 | 91 | 93 | 95 | 97 |
| 历史分数y | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若p,则q”与命题“若非q,则非p”互为逆否命题 | |
| B. | 命题“?x∈R,x3-x2-1≤0”的否定是“?x∈R,x3-x2-1>0” | |
| C. | “若f′(x)=0,则x为y=f(x)的极值点”为真命题 | |
| D. | “am2<bm2”是“a<b”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
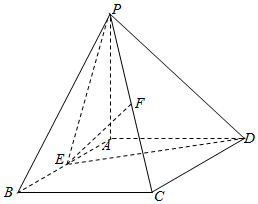 如图,已知四棱锥P-ABCD的底面为矩形,PA=AD=1,AB=2,且PA⊥平面ABCD,E,F分别为AB,PC的中点.
如图,已知四棱锥P-ABCD的底面为矩形,PA=AD=1,AB=2,且PA⊥平面ABCD,E,F分别为AB,PC的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com