
| 学生编号 | 1 | 2 | 3 | 4 | 5 |
| 政治分数x | 89 | 91 | 93 | 95 | 97 |
| 历史分数y | 87 | 89 | 89 | 92 | 93 |
分析 (1)做出女生和男生在总人数中所占的比例,用比例乘以要抽取的样本容量,得到结果.
(2)先求出两个变量的平均数,再利用最小二乘法做出线性回归方程的系数,把做出的系数和x,y的平均数代入公式,求出a的值,写出线性回归方程,得到结果.
解答 解:(1)男生5×$\frac{24}{60}$=2人,女生5×$\frac{36}{60}$=3人;
(2)可求得:$\overline{x}$=$\frac{1}{5}$(89+91+93+95+97)=93,$\overline{y}$=$\frac{1}{5}$(87+89+89+92+93)=90,
$\sum_{i=1}^{5}$$({x}_{i}-\overline{x})^{2}$=40,$\sum_{i=1}^{5}$$({y}_{i}-\overline{y})^{2}$=24,$\sum_{i=1}^{5}$$({x}_{i}-\overline{x})({y}_{i}-\overline{y})$=30,
r=$\frac{30}{\sqrt{40×24}}$≈0.97,有较强的线性相关关系,
b=$\frac{30}{40}$=0.75,a=20.25,线性回归方程是y=0.75x+20.25.
点评 本题考查线性回归分析的初步应用,考查分层抽样,考查了学生的数据处理能力和应用意识,考查利用数学知识解决实际问题的能力,是一个比较好的综合题目.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:选择题
| A. | ②③④ | B. | ①②④ | C. | ①③④ | D. | ①②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
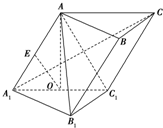 如图,在斜三棱柱ABC-A1B1C1中,点O、E分别是A1C1、AA1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.
如图,在斜三棱柱ABC-A1B1C1中,点O、E分别是A1C1、AA1的中点,AO⊥平面A1B1C1.已知∠BCA=90°,AA1=AC=BC=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
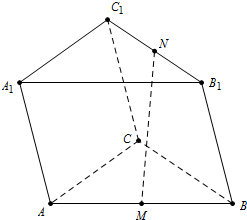
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com