解:(Ⅰ)定义域为{x|x>-1},
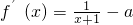
(1分)
①当a=0时,∵
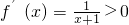
,
∴f(x)的单调递增区间为(-1,+∞)(2分)
②当a<0时,
∵

∴f(x)的单调递增区间为(-1,+∞)(3分)
③当a>0时,由f′(x)>0,则
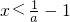
,
所以f(x)的单调递增区间为

,
由f′(x)<0,则
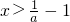
,
所以f(x)的单调递减区间为
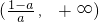
(4分)
(Ⅱ)当a=1时,f(x)=ln(x+1)-x,
由(Ⅰ)可知f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,
所以

(5分)
由表可知f(x)的最大值为f(0)=0(6分)
(Ⅲ)由(Ⅱ)可知f(x)=ln(x+1)-x≤0(*)
两边取对数可知
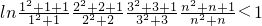
即证
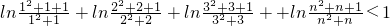
又
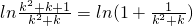
由(*)式可知当x≠0时,ln(1+x)<x(9分)
∴
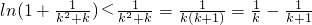
∴

=

(12分)
∴原不等式得证
分析:解:(1)先确定定义域,再用导数法求单调区间;要注意a的讨论,
(2)当a=1时,f(x)=ln(x+1)-x,由(1)可知f(x)在(-1,0)上单调递增,在(0,+∞)上单调递减,从而求得其最大值.
(3)对
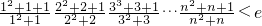
两边取对数,将问题转化为证明
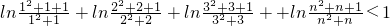
,由(x)=ln(x+1)-x≤0得证.
点评:本题主要考查导数法求单调区间,求函数最值,同时提醒学生在综合题中已证结论可以用到下一问题去解决问题.

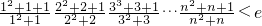 .
.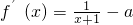 (1分)
(1分)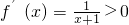 ,
,
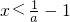 ,
, ,
,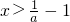 ,
,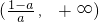 (4分)
(4分) (5分)
(5分)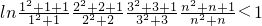
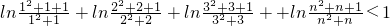
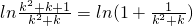 由(*)式可知当x≠0时,ln(1+x)<x(9分)
由(*)式可知当x≠0时,ln(1+x)<x(9分)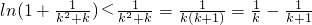

 (12分)
(12分)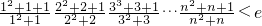 两边取对数,将问题转化为证明
两边取对数,将问题转化为证明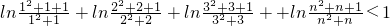 ,由(x)=ln(x+1)-x≤0得证.
,由(x)=ln(x+1)-x≤0得证.
