
一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为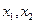 ,记
,记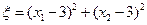 .
.
(1)分别求出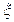 取得最大值和最小值时的概率; (2)
取得最大值和最小值时的概率; (2) 求
求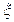 的分布列及数学期望.
的分布列及数学期望.
 解:(1)掷出点数
解:(1)掷出点数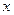 可能是:
可能是: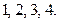 则
则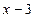 分别得:
分别得: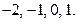 于是
于是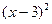 的所有取值分别为:
的所有取值分别为: 因此
因此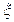 的所有取值为:0,1,2,4
的所有取值为:0,1,2,4 ,5,8. 3分
,5,8. 3分
当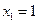 且
且 时,
时,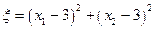 可取得最大值
可取得最大值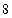 ,
,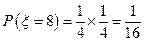 ; …………………………5分
; …………………………5分 
当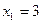 且
且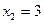 时,
时,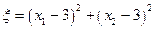 可取得最小值
可取得最小值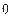 ,
,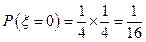 . …………………………7分
. …………………………7分
(2)由(Ⅰ)知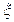 的所有取值为:0,1,2,4,5,8.
的所有取值为:0,1,2,4,5,8. 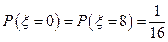 ;
;
当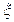 =1时,
=1时,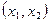 的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即
的所有取值为(2,3)、(4,3)、(3,2)、(3,4).即 ;
;
当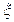 =2时,
=2时,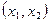 的所有取值为(2,2)、(4,4)、(4,2)、(2,4)即
的所有取值为(2,2)、(4,4)、(4,2)、(2,4)即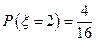 ;
;
当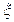 =4时,
=4时,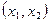 的所有取值为(1,3)、(3,1).即
的所有取值为(1,3)、(3,1).即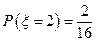 ;
;
当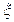 =5时,
=5时,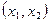 的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即
的所有取值为(2,1)、(1,4)、(1,2)、(4,1).即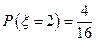 .
.
所以ξ的分布列为:……12分ξ 0 1  2
24 5 8 P 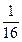
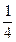
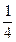
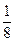
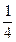
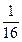
解析


科目:高中数学 来源: 题型:解答题
现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对楼市“楼市限购令”赞成人数如下表.
| 月收入(单位百元) | [15,25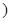 | [25,35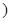 | [35,45 | [45,55 | [55,65 | [65,75 |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
| | 月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 |
| 赞成 | 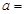 | 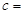 | |
| 不赞成 |  | 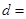 | |
| 合计 | | | |
 ,求随机变量
,求随机变量 的分布列及数学期望。
的分布列及数学期望。查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在奥运会射箭决赛中,参赛号码为1~4号的四名射箭运动员参加射箭比赛.
(Ⅰ)通过抽签将他们安排到1~4号靶位,试求恰有两名运动员所抽靶位号与其参赛号码相同的概率;
(Ⅱ)记1号、2号射箭运动员射箭的环数为 (
( 所有取值为0,1,2,3...,10)的概率分别为
所有取值为0,1,2,3...,10)的概率分别为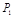 、
、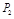 .根据教练员提供的资料,其概率分布如下表:
.根据教练员提供的资料,其概率分布如下表:
 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
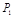 | 0 | 0 | 0 | 0 | 0.06 | 0.04 | 0.06 | 0.3 | 0.2 | 0.3 | 0.04 |
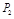 | 0 | 0 | 0 | 0 | 0.04 | 0.05 | 0.05 | 0.2 | 0.32 | 0.32 | 0.02 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
( 12分)
甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约,甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设甲面试合格的概率为 ,乙、丙面试合格的概率都是
,乙、丙面试合格的概率都是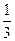 ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(1)至少有1人面试合格的概率;
(2)签约人数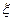 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分) 甲、乙两位篮球运动员进行定点投蓝,每人各投4个球,甲投篮命中的概率为 ,乙投篮命中的概率为
,乙投篮命中的概率为 .
.
(1)求甲至多命中2个且乙至少命中2个的概率;
(2)若规定每投篮一次命中得3分,未命中得 分,求乙所得分数
分,求乙所得分数 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com