
分析 由题意可得,m为正实数,根据f(-x)=-f(x),可得n=±2.再由n≠-2可得n=2.再由函数的解析式解求得函数的定义域为(-$\frac{1}{2}$,$\frac{1}{2}$).根据函数f(x)定义在区间[-m,m]上,可得0<m<$\frac{1}{2}$,从而求得nm 的范围.
解答 解:由题意可得,m为正实数,f(-x)=-f(x),化简可得$lo{g}_{2}\frac{1-(nx)^{2}}{1-4{x}^{2}}$=0,n=±2.
∵n≠-2,∴n=2,函数的解析式为f(x)=log2$\frac{1+2x}{1-2x}$,可得$\frac{1+2x}{1-2x}$>0,即(2x+1)(2x-1)<0,
解得-$\frac{1}{2}$<x<$\frac{1}{2}$,故函数的定义域为 (-$\frac{1}{2}$,$\frac{1}{2}$).
再由函数f(x)定义在区间[-m,m]上,可得0<m<$\frac{1}{2}$,故1<nm<$\sqrt{2}$,
故答案为:(1,$\sqrt{2}$).
点评 本题主要求函数的奇偶性,求函数的定义域,不等式的性质,属于基础题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 8 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
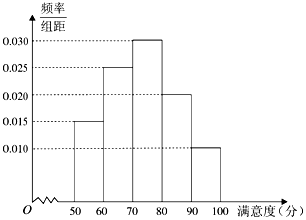 某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:
某校学生营养餐由A和B两家配餐公司配送.学校为了解学生对这两家配餐公司的满意度,采用问卷的形式,随机抽取了40名学生对两家公司分别评分.根据收集的80份问卷的评分,得到如图A公司满意度评分的频率分布直方图和如表B公司满意度评分的频数分布表:| 满意度 评分分组 | 频数 |
| [50,60) | 2 |
| [60,70) | 8 |
| [70,80) | 14 |
| [80,90) | 14 |
| [90,100] | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3,2} | B. | {-3,0,2} | C. | {3,-2} | D. | {3,0,-2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )
如图所示,单位位圆上的两个向量$\overrightarrow{a},\overrightarrow{b}$相互垂直,若向量$\overrightarrow{c}$满足($\overrightarrow{c}-\overrightarrow{a}$)•($\overrightarrow{c}-\overrightarrow{b}$)=0,则|$\overrightarrow{c}$|的取值范围是( )| A. | [0,1] | B. | [0,$\sqrt{2}$] | C. | [1,$\sqrt{2}$] | D. | [1,2] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com