
分析 (1)由a=1时,求得f(x)的解析式,当x≥1时,由二次函数的对称轴可知:x=-$\frac{b}{2a}$=$\frac{1}{2}$,根据函数的单调性f(x)≥f(1)=1;当x<1时,f(x)≥f(-$\frac{1}{2}$)=-$\frac{5}{4}$. 即可求得函数f(x)的最小值;
(2)当a<0时,设h(x)=f(x)-g(x)=x2-a|x-1|-|x-a|,求得函数的g(x)的解析式,分类,根据二次函数图象及性质即可求得函数的解的个数.
解答 解:(1)由a=1时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-x+1,x≥1}\\{{x}^{2}+x-1,x<1}\end{array}\right.$,
当x≥1时,由二次函数的对称轴可知:x=-$\frac{b}{2a}$=$\frac{1}{2}$,
∴f(x)≥f(1)=1;
当x<1时,由二次函数的对称轴可知:x=-$\frac{b}{2a}$=$\frac{1}{2}$,
f(x)≥f(-$\frac{1}{2}$)=-$\frac{5}{4}$.
所以,f(x)min=f(-$\frac{1}{2}$)=-$\frac{5}{4}$;
(2)当a<0时,设h(x)=f(x)-g(x)=x2-a|x-1|-|x-a|;
a<0时,h(x)=$\left\{\begin{array}{l}{{x}^{2}-(a+1)x+2a,x≥1}\\{{x}^{2}+(a-1)x,a≤x<1}\\{{x}^{2}+(a+1)x-2a,x<a}\end{array}\right.$,
x≥1时,h(1)=a<0.
∴x≥1时,一个零点.
a≤x<1时,解得:x1=0,x2=1-a>1,(舍去)
所以,当a≤x<1时,有且仅有一个零点.
x<a时,△=a2+10a+1,对称轴x=-$\frac{a+1}{2}$,h(a)=a(2a-1)>0,
所以(ⅰ)a≤-$\frac{1}{3}$时,△>0,对称轴x=-$\frac{a+1}{2}$≥a,无零点;
(ⅱ)-$\frac{1}{3}$<a<-5+2$\sqrt{6}$时,△=a2+10a+1<0,无零点;
(ⅲ)a=-5+2$\sqrt{6}$时,x=2-$\sqrt{6}$<a=-5+2$\sqrt{6}$,一个零点;
(ⅳ)-5+2$\sqrt{6}$<a<0时,
△=a2+10a+1>0,对称轴x=-$\frac{a+1}{2}$<a,两个零点.
综上,(ⅰ)a<-5+2$\sqrt{6}$时,y=f(x)与y=g(x)的图象的公共点有2个;
(ⅱ)a=-5+2$\sqrt{6}$时,y=f(x)与y=g(x)的图象的公共点有3个;
(ⅲ)-5+2$\sqrt{6}$<a<0时,y=f(x)与y=g(x)的图象的公共点有4个.
点评 本题考查考查二次函数的图象及性质,考查分段函数及绝对值函数的应用,考查函数的解析式应用,考查计算能力,考查分类讨论思想,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{27}$ | B. | -$\frac{2}{27}$ | C. | $\frac{2}{27}$ | D. | $\frac{4}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<a<b | B. | c<b<a | C. | a<b<c | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{9}{2}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
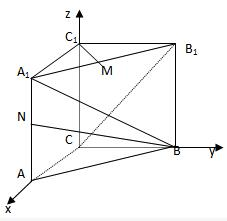 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com