
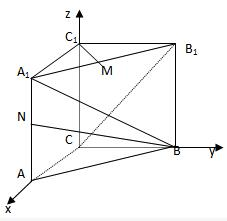
 如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图所示,直三棱柱ABC-A1B1C1中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.分析 (1)我们求出向量$\overrightarrow{{BA}_{1}}$,$\overrightarrow{{C}_{1}M}$的坐标,然后代入向量数量积公式,判定两个向量的数量积是否为0,若成立,则表明A1B⊥C1M
(2)分别求出向量$\overrightarrow{{BA}_{1}}$,$\overrightarrow{{CB}_{1}}$的坐标,然后代入两个向量夹角余弦公式,即可得到cos<$\overrightarrow{{BA}_{1}}$,$\overrightarrow{{CB}_{1}}$>的值;
解答 解:如图,以C为原点建立空间直角坐标系O-xyz.
(1)证明:依题意得A1(1,0,2),B(0,1,0),C1(0,0,2),M($\frac{1}{2}$,$\frac{1}{2}$,2),
∴$\overrightarrow{{A}_{1}B}$=(-1,1,-2),$\overrightarrow{{C}_{1}M}$=($\frac{1}{2}$,$\frac{1}{2}$,0),
∴$\overrightarrow{{A}_{1}B}$•$\overrightarrow{{C}_{1}M}$=-$\frac{1}{2}$+$\frac{1}{2}$+0=0,
∴$\overrightarrow{{A}_{1}B}$⊥$\overrightarrow{{C}_{1}M}$(6分)
(2)依题意得C(0,0,0),B1(0,1,2).
∴$\overrightarrow{{BA}_{1}}$=(1,-1,2),$\overrightarrow{{CB}_{1}}$=(0,1,2),
∴$\overrightarrow{{BA}_{1}}$•$\overrightarrow{{CB}_{1}}$=3,|$\overrightarrow{{BA}_{1}}$|=$\sqrt{6}$,|$\overrightarrow{{CB}_{1}}$|=$\sqrt{5}$(9分)
∴cos<$\overrightarrow{{BA}_{1}}$,$\overrightarrow{{CB}_{1}}$>=$\frac{|\overrightarrow{{BA}_{1}}•\overrightarrow{{CB}_{1}}|}{\left|\overrightarrow{{BA}_{1}}\right|•\left|\overrightarrow{{CB}_{1}}\right|}$=$\frac{3}{\sqrt{30}}$=$\frac{\sqrt{30}}{10}$(12分)
点评 本小题主要考查空间向量及运算的基本知识,空间中点、线、面的距离计算,空间两点间距离公式,异面直线及其所成的角,其中建立空间坐标系,确定各点坐标,及直线方向向量的坐标是解答本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①简单随机抽样②系统抽样 | B. | ①分层抽样 ②简单随机抽样 | ||
| C. | ①系统抽样②分层抽样 | D. | ①分层抽样②系统抽样 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | -8 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 | 7 |
| y | 4 | 2.5 | -0.5 | 0.5 | -2 |
| A. | 增加0.9个单位 | B. | 减少0.9个单位 | C. | 增加1个单位 | D. | 减少1个单位 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com