
���� ��1���ɹ�F1��ֱ������Բ����A��B���㣬��ABF2���ܳ�Ϊ8���ɵ�4a=8����������e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��a2=b2+c2������������ɣ�
��2��0��t��2����x=t������Բ���̿ɵ�y2=1-$\frac{{t}^{2}}{4}$���ɵ�M$��t��\frac{\sqrt{4-{t}^{2}}}{2}��$��$N��t��-\frac{\sqrt{4-{t}^{2}}}{2}��$����MNΪֱ����Բ�ı�����Ϊ����x-t��2+y2=1-$\frac{{t}^{2}}{4}$������Բ���������ɵã�3x2-8tx+5t2=0�����xP=$\frac{5t}{3}$��2��$0��t��\frac{6}{5}$����ˡ�MNP�����S��t��=$\frac{1}{2}|MN|•{x}_{P}$=$\frac{1}{3}\sqrt{-��{t}^{2}-2��^{2}+4}$�����ö��κ����ĵ����Լ��ɵó���
��� �⣺��1���߹�F1��ֱ������Բ����A��B���㣬��ABF2���ܳ�Ϊ8��
��4a=8�����a=2��
��������e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$��a2=b2+c2��
���c=$\sqrt{3}$��b=1��
����ԲC�ı�����Ϊ$\frac{{x}^{2}}{4}+{y}^{2}$=1��
��2��0��t��2��
��x=t������Բ���̿ɵ�y2=1-$\frac{{t}^{2}}{4}$����y=��$\frac{\sqrt{4-{t}^{2}}}{2}$��M$��t��\frac{\sqrt{4-{t}^{2}}}{2}��$��$N��t��-\frac{\sqrt{4-{t}^{2}}}{2}��$��
����MNΪֱ����Բ�ı�����Ϊ����x-t��2+y2=1-$\frac{{t}^{2}}{4}$��
����$\left\{\begin{array}{l}{��x-t��^{2}+{y}^{2}=1-\frac{{t}^{2}}{4}}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$��
��Ϊ3x2-8tx+5t2=0��
���x=t����x=$\frac{5t}{3}$��
��xP=$\frac{5t}{3}$��
��$\frac{5t}{3}$��2�����$0��t��\frac{6}{5}$��
���MNP�����S��t��=$\frac{1}{2}��2��\frac{\sqrt{4-{t}^{2}}}{2}����\frac{5t}{3}-t��$=$\frac{1}{3}\sqrt{4-{t}^{2}}•t$=$\frac{1}{3}\sqrt{-��{t}^{2}-2��^{2}+4}$��
��h��t��=-��t2-2��2+4��$0��t��\frac{6}{5}$�ڵ���������
�൱t=$\frac{6}{5}$ʱ��h��t��ȡ�����ֵ����ʱS��t��Ҳȡ�����ֵ$\frac{16}{25}$��
���� ���⿼����Բ����Բ�ı����̼������ʡ�ֱ������Բ�ཻ���⡢�����ε�������㹫ʽ�����κ����ĵ����ԣ���������������������������������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | e | D�� | e+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
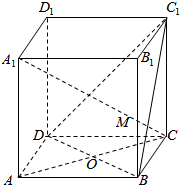 ��֪��������ABCD-A1B1C1D1�У�O��DB���е㣬ֱ��A1C��ƽ��C1BD�ڵ�M���ж����н����Ƿ���ȷ��
��֪��������ABCD-A1B1C1D1�У�O��DB���е㣬ֱ��A1C��ƽ��C1BD�ڵ�M���ж����н����Ƿ���ȷ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
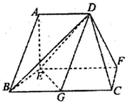 ����ͼ��ʾ�Ķ������У�����BCFE�����Σ�EF��BC��EF��EB��ƽ��ABE��ƽ��BCFE���ɵĽ�Ϊֱ����ǣ�AD��EF��BC=2AD=4��EF=3��AE=BE=2��AB=2$\sqrt{2}$��GΪBC�е㣮
����ͼ��ʾ�Ķ������У�����BCFE�����Σ�EF��BC��EF��EB��ƽ��ABE��ƽ��BCFE���ɵĽ�Ϊֱ����ǣ�AD��EF��BC=2AD=4��EF=3��AE=BE=2��AB=2$\sqrt{2}$��GΪBC�е㣮�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com