
【题目】(本小题满分14分)如图,三角形![]() 所在的平面与长方形
所在的平面与长方形![]() 所在的平面垂直,
所在的平面垂直,![]() ,
,![]() ,
,![]() .
.

(1)证明:![]() 平面
平面![]() ;
;
(2)证明:![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)由四边形![]() 是长方形可证
是长方形可证![]() ,进而可证
,进而可证![]() 平面
平面![]() ;(2)先证
;(2)先证![]() ,再证
,再证![]() 平面
平面![]() ,进而可证
,进而可证![]() ;(3)取
;(3)取![]() 的中点
的中点![]() ,连结
,连结![]() 和
和![]() ,先证
,先证![]() 平面
平面![]() ,再设点
,再设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,利用
,利用![]() 可得
可得![]() 的值,进而可得点
的值,进而可得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:(1)因为四边形![]() 是长方形,所以
是长方形,所以![]() ,因为
,因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(2)因为四边形![]() 是长方形,所以
是长方形,所以![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]()
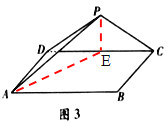
(3)取![]() 的中点
的中点![]() ,连结
,连结![]() 和
和![]() ,因为
,因为![]() ,所以
,所以![]() ,在
,在![]() 中,
中,![]()
![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,由(2)知:
,由(2)知:![]() 平面
平面![]() ,由(1)知:
,由(1)知:![]() ,所以
,所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,所以
,所以![]() ,设点
,设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,因为
,因为![]() ,所以
,所以![]() ,即
,即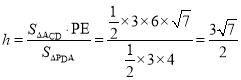 ,所以点
,所以点![]() 到平面
到平面![]() 的距离是
的距离是![]()


科目:高中数学 来源: 题型:
【题目】(本小题满分12分)
如图在直三棱柱ABC—A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的
中点.
(1) 求证: AC⊥BC1
(2) 求证:AC1∥平面CDB1
(3) 求异面直线AC1与B1C所成角的余弦值.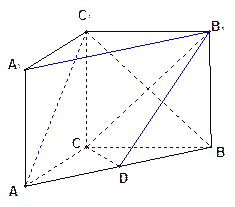
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 上一点
上一点![]() 关于直线
关于直线![]() 的对称点仍在圆
的对称点仍在圆![]() 上,直线
上,直线![]() 截得圆
截得圆![]() 的弦长为
的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设![]() 是直线
是直线![]() 上的动点,
上的动点,![]()
![]() 是圆
是圆![]() 的两条切线,
的两条切线,![]()
![]() 为切点,求四边形
为切点,求四边形![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中,错误的是( )

A.AC⊥SB
B.BC∥平面SAD
C.SA和SC与平面SBD所成的角相等
D.异面直线AB与SC所成的角和异面直线CD与SA所成的角相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“现代五项”是由现代奥林匹克之父顾拜旦先生创立的运动项目,包含射击、击剑、游泳、马术和越野五项运动.规定每一项运动的前三名得分都分别为![]() ,
,![]() ,
,![]() (
(![]() ,且
,且![]() ),每位选手各项得分之和为最终得分.在一次比赛中,只有甲、乙、丙三人参加“现代五项”,甲最终得22分,乙和丙最终各得9分,且乙的马术比赛获得了第一名.则:
),每位选手各项得分之和为最终得分.在一次比赛中,只有甲、乙、丙三人参加“现代五项”,甲最终得22分,乙和丙最终各得9分,且乙的马术比赛获得了第一名.则:![]() __________,游泳比赛的第三名是__________.
__________,游泳比赛的第三名是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两地相距1000![]() ,货车从甲地匀速行驶到乙地,速度不得超过80
,货车从甲地匀速行驶到乙地,速度不得超过80![]() ,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的
,已知货车每小时的运输成本(单位:元)由可变成本和固定成本组成,可变成本是速度平方的![]() 倍,固定成本为
倍,固定成本为![]() 元.
元.
(Ⅰ)将全程运输成本![]() (元)表示为速度
(元)表示为速度![]() (
(![]() )的函数,并指出这个函数的定义域;
)的函数,并指出这个函数的定义域;
(Ⅱ)为了使全程运输成本最小,货车应以多大的速度行驶?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 与两个定点
与两个定点![]() ,
,![]() 的距离的比为
的距离的比为![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 、
、![]() 两点,求线段
两点,求线段![]() 长度的最小值;
长度的最小值;
(3)已知圆![]() 的圆心为
的圆心为![]() ,且圆
,且圆![]() 与
与![]() 轴相切,若圆
轴相切,若圆![]() 与曲线
与曲线![]() 有公共点,求实数
有公共点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com