【题目】已知椭圆
的离心率为
，以椭圆的短轴为直径的圆与直线
相切.
（Ⅰ）求椭圆
的方程；
（Ⅱ）设椭圆过右焦点
的弦为
、过原点的弦为
，若
，求证：
为定值.
【答案】(Ⅰ) 
；(Ⅱ)证明见解析.
【解析】
试题分析：
(Ⅰ)由题意结合点到直线距离公式可得
.结合离心率计算公式有
.则椭圆
的方程为.
(Ⅱ)对直线的斜率分类讨论：当直线
的斜率不存在时，
.当直线的斜率存在时，设
，
，
，
，联立直线方程与椭圆方程有
，由弦长公式可得
.联立直线
与椭圆方程，结合弦长公式有
.计算可得.据此可得：为定值.
试题解析：
（Ⅰ）依题意，原点到直线
的距离为
，
则有.
由
，得
.
∴椭圆的方程为.
（Ⅱ）证明：（1）当直线的斜率不存在时，易求
，
，
则.
（2）当直线的斜率存在时，
设直线的斜率为
，依题意
，
则直线的方程为
，直线
的方程为.
设，，，，
由
得，
则
，
，
.
由
整理得
，则
.
.
∴
.
综合（1）（2），为定值.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】德国著名数学家狄利克雷在数学领域成就显著，以其名命名的函数
被称为狄利克雷函数，其中
为实数集，
为有理数集，则关于函数
有如下四个命题：①
；②函数是偶函数；③任取一个不为零的有理数
，
对任意的
恒成立；④存在三个点
，
，
，使得
为等边三角形.其中真命题的个数有（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数g(x)＝Acos(ωx＋φ)＋B的部分图象如图所示，将函数g(x)的图象保持纵坐标不变，横坐标向右平移
个单位长度后得到函数f(x)的图象．求：
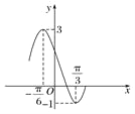
(1)函数f(x)在
上的值域；
(2)使f(x)≥2成立的x的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图是一几何体的平面展开图,其中
为正方形,
分别为
的中点,在此几何体中,给出下面四个结论:①直线
与直线
异面;②直线与直线
异面;③直线
平面
;④平面
平面
;其中正确的是_____.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在本市某旧小区改造工程中，需要在地下铺设天燃气管道.已知小区某处三幢房屋分别位于扇形
的三个顶点上，点
是弧
的中点，现欲在线段
上找一处开挖工作坑
（不与点
，重合），为铺设三条地下天燃气管线
，
，
，已知
米，
，记
，该三条地下天燃气管线的总长度为
米.
（1）将表示成
的函数，并写出的范围；
（2）请确定工作坑的位置，使此处地下天燃气管线的总长度最小，并求出总长度的最小值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】甲同学参加化学竞赛初赛，考试分为笔试、口试、实验三个项目，各单项通过考试的概率依次为
、
、
，笔试、口试、实验通过考试分别记4分、2分、4分，没通过的项目记0分，各项成绩互不影响.
（Ⅰ）若规定总分不低于8分即可进入复赛，求甲同学进入复赛的概率；
（Ⅱ）记三个项目中通过考试的个数为
，求随机变量的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
