
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,准线为
,准线为![]() ,过
,过![]() 的直线与
的直线与![]() 相交于
相交于![]() 两点.
两点.
(1)以![]() 为直径的圆与
为直径的圆与![]() 轴交
轴交![]() 两点,若
两点,若![]() ,求
,求![]() ;
;
(2)点![]() 在
在![]() 上,过点
上,过点![]() 且垂直于
且垂直于![]() 轴的直线与
轴的直线与![]() 分别相交于
分别相交于![]() 两点,证明:
两点,证明:![]() .
.
【答案】(1)![]() ;(2)证明见解析.
;(2)证明见解析.
【解析】
(1)根据题意,设![]() 的中点为
的中点为![]() ,
,![]() 在
在![]() 上的射影分别为
上的射影分别为![]() ,根据抛物线的性质得出
,根据抛物线的性质得出![]() ,得出
,得出![]() 到
到![]() 轴的距离
轴的距离![]() ,最后利用直线与圆的弦长公式得出
,最后利用直线与圆的弦长公式得出![]() ,代入数据即可得出结果;
,代入数据即可得出结果;
(2)设直线![]()
![]() ,联立直线和抛物线方程,求出韦达定理
,联立直线和抛物线方程,求出韦达定理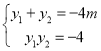 ,求出直线
,求出直线![]() 的方程,从而分别求出
的方程,从而分别求出![]() 两点的坐标,将证明
两点的坐标,将证明![]() 转化为证明
转化为证明![]() 成立即可,结合韦达定理即可证出.
成立即可,结合韦达定理即可证出.
解:(1)由题可知,![]() ,以
,以![]() 为直径的圆的半径为5,
为直径的圆的半径为5,
设![]() 的中点为
的中点为![]() ,即圆心为
,即圆心为![]() ,
,![]() 在
在![]() 上的射影分别为
上的射影分别为![]() ,
,
则![]()
![]()
![]() ,
,
所以![]() 到
到![]() 轴的距离
轴的距离![]() ,
,
故![]()
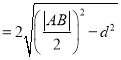
![]()
![]() .
.
(2)当直线![]() 斜率为0时,不满足题意;
斜率为0时,不满足题意;
则直线![]() 斜率不为0,设直线
斜率不为0,设直线![]()
![]() ,
,
设![]() ,
,![]() ,
,
由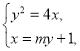 得
得![]() ,
,
所以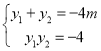 ,
,
直线![]()
![]() ,
,
令![]() ,得
,得![]()
![]()
![]() ,
,
即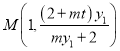 ,
,
同理可得: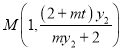 ,
,
要证![]() ,即证
,即证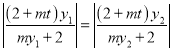 ,
,
又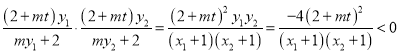 ,
,
即证![]() ,
,
即证![]() ,
,
即证![]() ,
,
即证![]() (※),
(※),
又因为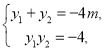
所以(※)式显然成立,故![]() ,命题得证.
,命题得证.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点
的焦点![]() 到准线
到准线![]() 的距离为2,直线
的距离为2,直线![]() 与抛物线交于不同的两点
与抛物线交于不同的两点![]() ,
,![]() .
.
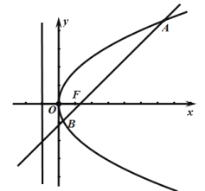
(1)求抛物线的方程;
(2)是否存在与![]() 的取值无关的定点
的取值无关的定点![]() ,使得直线
,使得直线![]() ,
,![]() 的斜率之和恒为定值?若存在,求出所有点
的斜率之和恒为定值?若存在,求出所有点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》是中国古代数学名著,由明代数学家程大位编著,它对我国民间普及珠算和数学知识起到了很大的作用,是东方古代数学的名著.在这部著作中,许多数学问题都是以歌诀形式呈现的,“九儿问甲歌”就是其中一首:“一个公公九个儿,若问生年总不知,自长排来差三岁,共年二百又零七,借问长儿多少岁,各儿岁数要详推.”这首歌决的大意是:“一位老公公有九个儿子,九个儿子从大到小排列,相邻两人的年龄差三岁,并且儿子们的年龄之和为207岁,请问大儿子多少岁,其他几个儿子年龄如何推算.”在这个问题中,记这位公公的第![]() 个儿子的年龄为
个儿子的年龄为![]() ,则
,则![]() ( )
( )
A.17B.29C.23D.35
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以坐标原点O为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:
轴的正半轴为极轴建立极坐标系,曲线C1的极坐标方程为:![]() ,曲线C2的参数方程为:
,曲线C2的参数方程为: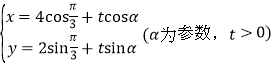 ,点N的极坐标为
,点N的极坐标为![]() .
.
(Ⅰ)若M是曲线C1上的动点,求M到定点N的距离的最小值;
(Ⅱ)若曲线C1与曲线C2有有两个不同交点,求正数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市场研究人员为了了解产业园引进的甲公司前期的经营状况,对该公司2018年连续六个月的利润进行了统计,并根据得到的数据绘制了相应的折线图,如图所示
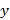
(1)由折线图可以看出,可用线性回归模型拟合月利润![]() (单位:百万元)与月份代码
(单位:百万元)与月份代码![]() 之间的关系,求
之间的关系,求![]() 关于
关于![]() 的线性回归方程,并预测该公司2019年3月份的利润;
的线性回归方程,并预测该公司2019年3月份的利润;
(2)甲公司新研制了一款产品,需要采购一批新型材料,现有![]() ,
,![]() 两种型号的新型材料可供选择,按规定每种新型材料最多可使用
两种型号的新型材料可供选择,按规定每种新型材料最多可使用![]() 个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对
个月,但新材料的不稳定性会导致材料损坏的年限不相同,现对![]() ,
,![]() 两种型号的新型材料对应的产品各
两种型号的新型材料对应的产品各![]() 件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
件进行科学模拟测试,得到两种新型材料使用寿命的频数统计如下表:
使用寿命 材料类型 |
|
|
|
| 总计 |
|
|
|
|
|
|
|
|
|
|
|
|
如果你是甲公司的负责人,你会选择采购哪款新型材料?
参考数据:![]() ,
,![]() .参考公式:回归直线方程为
.参考公式:回归直线方程为![]() ,其中
,其中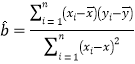
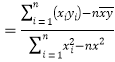 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com