
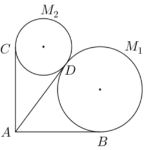
 某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;
某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;分析 (1)直接利用三角函数,可得结论;
(2)设∠BAD=2α,则总造价y=0.8•2π•60tanα+0.9•2π•60tan(45°-α),换元,利用基本不等式,可得结论.
解答 解:(1)M1半径=60tan30°≈34.6,M2半径=60tan15°≈16.1;
(2)设∠BAD=2α,则总造价y=0.8•2π•60tanα+0.9•2π•60tan(45°-α),
设1+tanα=x,则y=12π•(8x+$\frac{18}{x}$-17)≥84π,当且仅当x=$\frac{3}{2}$,tanα=$\frac{1}{2}$时,取等号,
∴M1半径30,M2半径20,造价263.8千元.
点评 本题考查直线与圆的位置关系,考查基本不等式的运用,属于中档题.


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(-∞,-\frac{1}{2}]∪[{0,\frac{3}{2}}]$ | B. | $[{\frac{1}{4},\frac{3}{2}}]$ | C. | $[{-\frac{1}{2},\frac{1}{4}}]$ | D. | $[{-\frac{1}{2},\frac{3}{2}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 | B. | 11 | C. | 15 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com