
分析 由函数的解析式、特殊角的三角函数值先求出$f(-\frac{π}{4})$的值,再求出$f(f(-\frac{π}{4}))$的值.
解答 解:由题意知,$f(x)=\left\{\begin{array}{l}{-\sqrt{2}sinx,-1≤x≤0}\\{tan(\frac{π}{4}x),0<x≤1}\end{array}\right.$,
则$f(-\frac{π}{4})$=$-\sqrt{2}×sin(-\frac{π}{4})$=$-\sqrt{2}×(-\frac{\sqrt{2}}{2})$=1,
所以f(1)=$tan\frac{π}{4}$=1,即$f(f(-\frac{π}{4}))$=1,
故答案为:1.
点评 本题考查分段函数的函数值,对于多层函数值应从内到外依次求值,注意自变量的范围,属于基础题.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
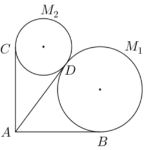 某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;
某景区欲建造两条圆形观景步道M1、M2(宽度忽略不计),如图所示,已知AB⊥AC,AB=AC=AD=60(单位:米),要求圆M1与AB、AD分别相切于点B、D,圆M2与AC、AD分别相切于点C、D;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点(-2,0)对称 | B. | 关于点(0,-2)对称 | ||
| C. | 关于直线x=-2对称 | D. | 关于直线x=0对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {0,1} | C. | {0,1,2} | D. | {-1,0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com