
分析 (1)把x=$\frac{1}{2}$代入方程ax2+2x+1=0求得a的值;然后再来解该一元二次方程;
(2)由已知中集合A={x∈R|ax2+2x+1=0},只有一个元素,根据集合元素的确定性,我们可以将问题转化为:关于x的方程ax2+2x+1=0有且只有一个解,分类讨论二次项系数a的值,结合二次方程根与△的关系,即可得到答案.
解答 解:(1)∵$\frac{1}{2}$∈A,∴$\frac{1}{2}$是方程ax2+2x+1=0的根,
∴$a{({\frac{1}{2}})^2}+2×\frac{1}{2}+1=0$,解得a=-8.∴方程为-8x2+2x+1=0.
∴x1=$\frac{1}{2}$,x2=-$\frac{1}{4}$,此时A=$\left\{{-\frac{1}{4},\frac{1}{2}}\right\}$.
(2)若a=0,则方程为2x+1=0,x=-$\frac{1}{2}$,A中仅有一个元素;
若a≠0,A中仅有一个元素,则△=4-4a=0,即a=1,方程有两个相等的实根
x1=x2=-1.
故所求集合B={0,1}.
点评 本题考查的知识点是集合元素的确定性及方程根的个数的判断及确定,其中根据元素的确定性,将问题转化为:关于x的方程ax2+2x+1=0有且只有一个解,是解答本题的关键.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
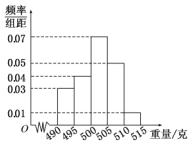 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9,+∞) | B. | (0,$\frac{1}{9}$] | C. | [$\frac{1}{9}$,+∞) | D. | (0,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{6}$ | B. | 2+2$\sqrt{2}$ | C. | $\frac{4\sqrt{6}}{3}$ | D. | 2$\sqrt{3}$+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com