
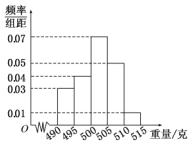
 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.分析 (1)由频率分布直方图,t先求出重量超过505克的产品所占频率,由此能求出重量超过505克的产品数量.
(2)抽取的40件产品中任取2件,设ξ为重量超过505克的产品数量,则ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
(3)一件产品的重量低于495克或超过510克都要重新包装,且把频率视作概率,则任取一件产品需要重新包装的概率为(0.03+0.01)×5=0.2,现在从该流水线上每间隔30分钟都随机地取出两件产品进行检测,则两件产品都不需要重新包装的概率为0.64,由此得到就目前的生产情况,该流水线需要停产.
解答 解:(1)由频率分布直方图,得重量超过505克的产品所占频率为:
(0.05+0.01)×5=0.3,
∴重量超过505克的产品数量为:0.3×40=12(件).
(2)抽取的40件产品中任取2件,设ξ为重量超过505克的产品数量,则ξ的可能取值为0,1,2,
P(ξ=0)=$\frac{{C}_{28}^{2}}{{C}_{40}^{2}}$=$\frac{63}{130}$,
P(ξ=1)=$\frac{{C}_{12}^{1}{C}_{28}^{1}}{{C}_{40}^{2}}$=$\frac{28}{65}$,
P(ξ=2)=$\frac{{C}_{12}^{2}}{{C}_{40}^{2}}$=$\frac{11}{130}$,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{63}{130}$ | $\frac{28}{65}$ | $\frac{11}{130}$ |
点评 本题考查频数的求法,考查离散型随机变量的分布列和数学期望的求法,考查概率的应用,是中档题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{11}{12}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com