
| A. | $\frac{11}{12}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{5}{6}$ |
分析 (1)由题意知本题是一个古典概型,事件(a,b)的基本事件有36个,方程组只有一个解,需满足2b-4a≠0,即b≠2a,而b=2a的事件有(1,2),(2,4),(3,6)共3个,根据古典概型概率公式得到结果
解答 解:(1)由题意知本题是一个古典概型,
事件(a,b)的基本事件有36个.
由方程组$\left\{\begin{array}{l}{ax+by=3}\\{2x+4y=7}\end{array}\right.$
可得$\left\{\begin{array}{l}{(2b-4a)x=8b-12}\\{(2b-4a)y=6-7a}\end{array}\right.$
方程组只有一个解,需满足2b-4a≠0,
即b≠2a,而b=2a的事件有(1,2),(2,4),(3,6)共3个,
所以方程组只有一个解的概率为P1=1-$\frac{3}{36}$=$\frac{11}{12}$,
故选A.
点评 本题考查古典概型,考查解方程组,是一个综合题,概率问题往往同其他的知识点结合在一起,实际上是以概率问题为载体,主要考查的是另一个知识点


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数f(x)=$\left\{\begin{array}{l}-\frac{1}{2}{x^2}-2x({x≤0})\\{(\frac{1}{2})^x}+1({x>0})\end{array}$.
已知函数f(x)=$\left\{\begin{array}{l}-\frac{1}{2}{x^2}-2x({x≤0})\\{(\frac{1}{2})^x}+1({x>0})\end{array}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0) | B. | (0,1) | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
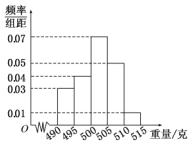 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com