
分析 由题意得这2个函数的周期完全相同,即$\frac{2π}{ω}$=$\frac{2π}{2}$,求得ω的值.再利用φ∈(0,π)以及正弦函数的定义域和值域,求得f(φ)的范围.
解答 解:∵函数f(x)=3sin(ωx-$\frac{π}{6}$)和g(x)=2sin(2x+φ)+1(ω>0,φ∈(0,π))的图象的对称轴完全相同,
故这2个函数的周期完全相同,即$\frac{2π}{ω}$=$\frac{2π}{2}$,∴ω=2.
当φ∈(0,π),所以2φ-$\frac{π}{6}$∈(-$\frac{π}{6}$,$\frac{11π}{6}$),由三角函数图象知:
f(φ)的最小值为3sin$\frac{3π}{2}$=-3,最大值为3sin$\frac{π}{2}$=3,
所以f(φ)的取值范围是[-3,3].
故答案为:[-3,3].
点评 本题考查三角函数的图象与性质,正弦函数的定义域和值域,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | a<b<c | B. | a<c<b | C. | b<a<c | D. | c<a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
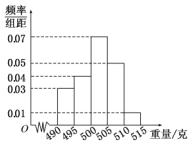 某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.
某食品厂为了检查一条自动包装流水线的生产情况,随机抽取该流水线上40件产品作为样本称出它们的重量(单位:克),重量的分组区间为 (490,495],(495,500],…,(510,515],由此得到样本的频率分布直方图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (9,+∞) | B. | (0,$\frac{1}{9}$] | C. | [$\frac{1}{9}$,+∞) | D. | (0,9] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a⊥α,b∥β,a⊥b,则α⊥β | B. | 若a⊥α,b∥β,a∥b,则α⊥β | ||
| C. | 若a⊥α,a⊥β,则α⊥β | D. | 若a∥β,b∥β,a∥b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com