
设满足以下两个条件得有穷数列 为
为 阶“期待数列”:
阶“期待数列”:
① ,②
,② .
.
(1)若等比数列 为
为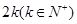 阶“期待数列”,求公比
阶“期待数列”,求公比 ;
;
(2)若一个等差数列 既为
既为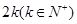 阶“期待数列”又是递增数列,求该数列的通项公式;
阶“期待数列”又是递增数列,求该数列的通项公式;
(3)记 阶“期待数列”
阶“期待数列” 的前
的前 项和为
项和为 .
.
( )求证:
)求证: ;
;
(
 )若存在
)若存在 ,使
,使 ,试问数列
,试问数列
 是否为
是否为 阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
阶“期待数列”?若能,求出所有这样的数列;若不能,请说明理由.
(1)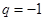 ;(2)
;(2)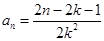 ;(3)(
;(3)(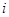 )证明见解析;(
)证明见解析;(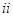 )不能,理由见解析.
)不能,理由见解析.
解析试题分析:
(1)由 阶“期待数列”定义,当
阶“期待数列”定义,当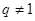 ,结合已知条件①求得等比数列的公比
,结合已知条件①求得等比数列的公比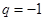 ,若
,若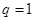 ,由①得,
,由①得, 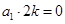 ,得
,得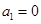 ,不可能,所以
,不可能,所以 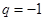 ;
;
(2)设出等差数列的公差,结合①②求出公差,再由前 项和为
项和为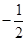 求出首项,则等差数列的通项公式可求;
求出首项,则等差数列的通项公式可求;
(3)(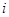 )由
)由 阶“期待数列”
阶“期待数列” 前
前 项中所有的和为0,所有项的绝对值之和为1,求得所有非负项的和为
项中所有的和为0,所有项的绝对值之和为1,求得所有非负项的和为 ,所有负项的和为
,所有负项的和为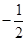 ,从而得到答案;
,从而得到答案;
(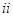 )借助于(
)借助于(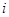 )中结论知,数列
)中结论知,数列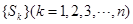 的前
的前 项和为
项和为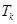 ,且满足
,且满足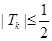 ,再由
,再由 ,得到
,得到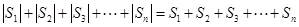 ,从而说明
,从而说明 与
与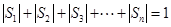 不能同时成立.
不能同时成立.
(1) 若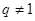 ,则由①
,则由①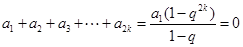
由 ,所以
,所以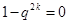 ,得
,得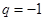 ,
,
由②得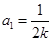 或
或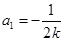 ,满足题意.
,满足题意.
若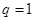 ,由①得,
,由①得, 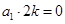 ,得
,得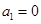 ,不可能.
,不可能.
综上所述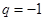 .
.
(2)设等差数列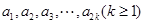 的公差为
的公差为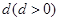 .
.
因为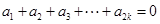 ,所以
,所以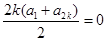 .
.
所以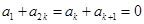 .
.
因为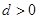 ,所以由
,所以由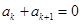 ,得
,得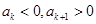 .
.
由题中的①、②得 ,
, 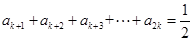 ,
,
两式相减得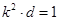 , 即
, 即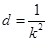 . 又
. 又 ,得
,得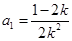 .
.
所以 .
.
(3) 记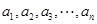 中非负项和为
中非负项和为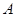 ,负项和为
,负项和为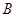 .
.
则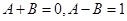 , 得
, 得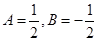 .
.
(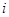 ) 因为
) 因为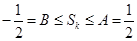 ,所以
,所以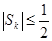 .
.
(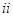 ) 若存在
) 若存在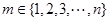 ,使
,使 ,由前面的证明过程知:
,由前面的证明过程知:  ,
,
且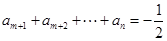 .
.
记数列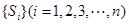 的前
的前

 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:解答题
已知数列{an}的前n项和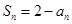 ,数列{bn}满足b1=1,b3+b7=18,且
,数列{bn}满足b1=1,b3+b7=18,且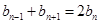 (n≥2).(1)求数列{an}和{bn}的通项公式;(2)若
(n≥2).(1)求数列{an}和{bn}的通项公式;(2)若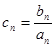 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(12分)(2011•福建)已知等差数列{an}中,a1=1,a3=﹣3.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若数列{an}的前k项和Sk=﹣35,求k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2011•浙江)已知公差不为0的等差数列{an}的首项a1为a(a∈R)设数列的前n项和为Sn,且 ,
, ,
, 成等比数列.
成等比数列.
(1)求数列{an}的通项公式及Sn;
(2)记An= +
+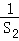 +
+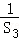 +…+
+…+ ,Bn=
,Bn= +
+ +…+
+…+ ,当n≥2时,试比较An与Bn的大小.
,当n≥2时,试比较An与Bn的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列{an}中,a1=2,an=2-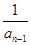 (n≥2,n∈N*).
(n≥2,n∈N*).
(1)设bn=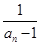 ,n∈N*,求证:数列{bn}是等差数列;
,n∈N*,求证:数列{bn}是等差数列;
(2)设cn=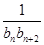 (n∈N*),求数列{cn}的前n项和Sn.
(n∈N*),求数列{cn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•浙江)在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(Ⅰ)求d,an;
(Ⅱ)若d<0,求|a1|+|a2|+|a3|+…+|an|.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•天津)已知首项为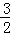 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设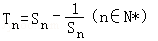 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com