
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分别为棱
分别为棱![]() 的中点.
的中点.
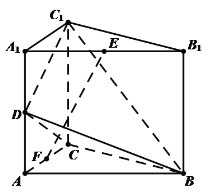
(1)求证:![]() ∥平面
∥平面![]()
(2)若异面直线![]() 与
与![]() 所成角为
所成角为![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在斜三梭柱ABC﹣A1B1C1中,侧面AA1C1C是菱形,AC1与A1C交于点O,E是棱AB上一点,且OE∥平面BCC1B1
(1)求证:E是AB中点;
(2)若AC1⊥A1B,求证:AC1⊥BC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果一个几何体的主视图与左视图是全等的长方形,边长分别是![]() ,如图所示,俯视图是一个边长为
,如图所示,俯视图是一个边长为![]() 的正方形.
的正方形.
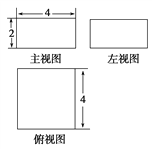
(1)求该几何体的表面积;
(2)求该几何体的外接球的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某山区小学有100名四年级学生,将全体四年级学生随机按00~99编号,并且按编号顺序平均分成10组.现要从中抽取10名学生,各组内抽取的编号按依次增加10进行系统抽样.

(1)若抽出的一个号码为22,则此号码所在的组数是多少?据此写出所有被抽出学生的号码;
(2)分别统计这10名学生的数学成绩,获得成绩数据的茎叶图如图4所示,求该样本的方差;
(3)在(2)的条件下,从这10名学生中随机抽取两名成绩不低于73分的学生,求被抽取到的两名学生的成绩之和不小于154分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学调查了某班全部 45 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 | 8 | 5 |
未参加书法社团 | 2 | 30 |
(1)从该班随机选 1 名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的 8 名同学中,有 5 名男同学![]() ,3名女同学
,3名女同学![]() .现从这 5 名男同学和 3 名女同学中各随机选 1 人,求
.现从这 5 名男同学和 3 名女同学中各随机选 1 人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O1和圆O2的极坐标方程分别为ρ=2, ![]() .
.
(1)把圆O1和圆O2的极坐标方程化为直角坐标方程;
(2)求经过两圆交点的直线的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某市有一条东西走向的公路l,现欲经过公路l上的O处铺设一条南北走向的公路m,在施工过程中发现O处的正北方向1百米的A处有一汉代古迹,为了保护古迹,该市委决定以A为圆心,1百米为半径设立一个圆形保护区,为了连通公路l,m,欲再新建一条公路PQ,点P,Q分别在公路l,m上(点P,Q分别在点O的正东、正北方向),且要求PQ与圆A相切.

(1)当点P距O处2百米时,求OQ的长;
(2)当公路PQ的长最短时,求OQ的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com