在平面直角坐标系xOy中,过原点O的直线与函数y=log8x的图象交于A、B两点(A在B的左侧),分别过A、B作y轴的平行线分别与函数y=log2x的图象交于C、D两点,若BC∥x轴,则四边形ABCD的面积为 .
【答案】
分析:设出A、B的坐标,求出OA、OB的斜率相等利用三点共线得出A、B的坐标之间的关系.再根据BC平行x轴,B、C纵坐标相等,推出横坐标的关系,结合之前得出A、B的坐标之间的关系即可求出A的坐标,从而解出B、C、D的坐标,最后利用梯形的面积公式求解即可.
解答: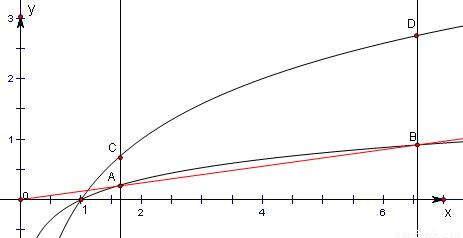
解:设点A、B的横坐标分别为x
1、x
2由题设知,x
1>1,x
2>1.
则点A、B纵坐标分别为log
8x
1、log
8x
2.
因为A、B在过点O的直线上,所以
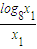
=
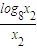
,
点C、D坐标分别为(x
1,log
2x
1),(x
2,log
2x
2).
由于BC平行于x轴知
log
2x
1=log
8x
2,
即得log
2x
1=

log
2x
2,
∴x
2=x
13.
代入x
2log
8x
1=x
1log
8x
2得x
13log
8x
1=3x
1log
8x
1.
由于x
1>1知log
8x
1≠0,
∴x
13=3x
1.
考虑x
1>1解得x
1=
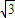
.
于是点A的坐标为(
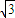
,log
8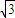
)即A(
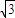
,

log
23)
∴B(3
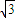
,

log
23),C(
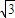
,

log
23),D(3
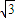
,

log
23).
∴梯形ABCD的面积为S=

(AC+BD)×BC=

(

log
23+log
23)×2
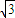
=

.
故答案为:
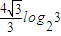
.
点评:本小题主要考查对数函数图象、对数换底公式、对数方程、指数方程等基础知识,考查运算能力和分析问题的能力.

 解:设点A、B的横坐标分别为x1、x2由题设知,x1>1,x2>1.
解:设点A、B的横坐标分别为x1、x2由题设知,x1>1,x2>1.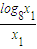 =
=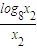 ,
, log2x2,
log2x2,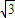 .
.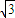 ,log8
,log8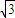 )即A(
)即A(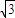 ,
, log23)
log23)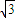 ,
, log23),C(
log23),C(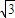 ,
, log23),D(3
log23),D(3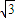 ,
, log23).
log23). (AC+BD)×BC=
(AC+BD)×BC= (
(  log23+log23)×2
log23+log23)×2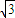 =
= .
.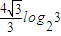 .
.

 53随堂测系列答案
53随堂测系列答案 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是