
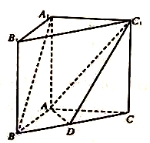
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点.
(1)求证:A1B∥平面ADC1;
(2)若AB=AC,BC=AA1=2,求点A1到平面ADC1的距离.
(1)见解析;(2)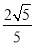
【解析】试题分析:(1)通过“平面外的直线平行于平面内的直线”证明线面平行;(2)直接求距离不方便时,可以利用等面积或者等体积方法求点到平面的而距离.
试题解析:(Ⅰ)连接A1C,交AC1于点E,则点E是A1C及AC1的中点.连接DE,则DE∥A1B.因为DE?平面ADC1,所以A1B∥平面ADC1. 4分
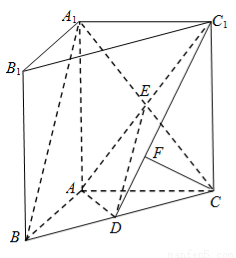
(Ⅱ)由(Ⅰ)知A1B∥平面ADC1,
则点A1与B到与平面ADC1的距离相等,又点D是BC的中点,点C与B到与平面ADC1的距离相等,则C到与平面ADC1的距离即为所求. 6分
因为AB=AC,点D是BC的中点,所以AD⊥BC,又AD⊥A1A,
所以AD⊥平面BCC1B1,平面ADC1⊥平面BCC1B1.
作于CF⊥DC1于F,则CF⊥平面ADC1,CF即为所求距离. 10分
在Rt△DCC1中,CF=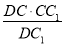 =
=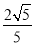 .
.
所以A1到与平面ADC1的距离为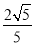 . 12分
. 12分
考点:空间几何体,空间线面平行,点到平面的距离


科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试理科数学试卷(解析版) 题型:选择题
设向量a,b满足|a|=|b|=|a+b|=1,则|a-tb|(t∈R)的最小值为( )
A.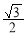 B.
B.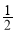 C.1 D.2
C.1 D.2
查看答案和解析>>
科目:高中数学 来源:2015届河北省唐山市高三年级摸底考试文科数学试卷(解析版) 题型:填空题
实数x,y满足x+2y=2,则3x+9y的最小值是________________.
查看答案和解析>>
科目:高中数学 来源:2015届河北省高二下学期期中考试理科数学试卷(解析版) 题型:选择题
已知函数 ,
,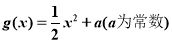 ,直线
,直线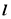 与 函数
与 函数 的图像都相切,且
的图像都相切,且 与函数
与函数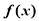 图像的切点的横坐标为1,则
图像的切点的横坐标为1,则 的值为 ( )
的值为 ( )
A.1 B. C.
C.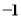 D.
D.
查看答案和解析>>
科目:高中数学 来源:2015届河北省保定市高二下学期期中考试理科数学试卷(解析版) 题型:填空题
在长方体ABCD-A1B1C1D1中,AB=2,BC=AA1=1,则D1C1与平面A1BC1所成角的正弦值为________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com