
【题目】已知函数f(x)=alnx﹣ax﹣3(a≠0).
(1)讨论f(x)的单调性;
(2)若f(x)+(a+1)x+4﹣e≤0对任意x∈[e,e2]恒成立,求实数a的取值范围(e为自然常数).
【答案】
(1)解:f′(x)= ![]() ﹣a=
﹣a= ![]() =
= ![]() (x>0),
(x>0),
当a>0时,f(x)的单调增区间为(0,1],单调减区间为[1,+∞);
当a<0时,f(x)的单调增区间为[1,+∞),单调减区间为(0,1]
(2)解:令F(x)=alnx﹣ax﹣3+(a+1)x+4﹣e=alnx+x+1﹣e,则F′(x)= ![]() ,
,
若﹣a≤e,即a≥﹣e,
F(x)在[e,e2]上是增函数,
F(x)max=F(e2)=2a+e2﹣e+1≤0,
a≤ ![]() (e﹣1﹣e2),无解.
(e﹣1﹣e2),无解.
若e<﹣a≤e2,即﹣e2≤a<﹣e,
F(x)在[e,﹣a]上是减函数;在[﹣a,e2]上是增函数,
F(e)=a+1≤0,即a≤﹣1.
F(e2)=2a+e2﹣e+1≤0,即a≤ ![]() (e﹣1﹣e2),
(e﹣1﹣e2),
∴﹣e2≤a≤ ![]() (e﹣1﹣e2).
(e﹣1﹣e2).
若﹣a>e2,即a<﹣e2,
F(x)在[e,e2]上是减函数,
F(x)max=F(e)=a+1≤0,即a≤﹣1,
∴a<﹣e2,
综上所述,a≤ ![]() (e﹣1﹣e2)
(e﹣1﹣e2)
【解析】(1)先求导,再分类讨论即可得到函数的单调性;(2)令F(x)=alnx﹣ax﹣3+(a+1)x+4﹣e=alnx+x+1﹣e,从而求导F′(x)= ![]() ,再由导数的正负讨论确定函数的单调性,从而求函数的最大值,从而化恒成立问题为最值问题即可.
,再由导数的正负讨论确定函数的单调性,从而求函数的最大值,从而化恒成立问题为最值问题即可.
【考点精析】利用利用导数研究函数的单调性和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明:MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从甲、乙两名运动员的若干次训练成绩中随机抽取6次,分别为
甲:7.7,7.8,8.1,8.6,9.3,9.5
乙:7.6,8.0,8.2,8.5,9.2,9.5
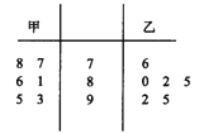
(1)根据以上的茎叶图,不用计算说一下甲乙谁的方差大,并说明谁的成绩稳定;
(2)从甲、乙运动员高于8.1分成绩中各随机抽取1次成绩,求甲、乙运动员的成绩至少有一个高于9.2分的概率.
(3)经过对甲、乙运动员若干次成绩进行统计,发现甲运动员成绩均匀分布在[7.5,9.5]之间,乙运动员成绩均匀分布在[7.0,10]之间,现甲、乙比赛一次,求甲、乙成绩之差的绝对值小于0.5分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的首项
的首项![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(Ⅰ)证明:![]() 是等比数列;
是等比数列;
(Ⅱ)若![]() ,数列
,数列![]() 中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(Ⅲ)若![]() 是递增数列,求
是递增数列,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若样本![]() 的平均数是
的平均数是![]() ,方差是
,方差是![]() ,则对样本
,则对样本![]() ,下列结论正确的是 ( )
,下列结论正确的是 ( )
A. 平均数为14,方差为5 B. 平均数为13,方差为25
C. 平均数为13,方差为5 D. 平均数为14,方差为2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com