
【题目】(本小题满分12分)
已知函数![]() (其中a是实数).
(其中a是实数).
(1)求![]() 的单调区间;
的单调区间;
(2)若设![]() ,且
,且![]() 有两个极值点
有两个极值点![]()
![]() ,求
,求![]() 取值范围.(其中e为自然对数的底数).
取值范围.(其中e为自然对数的底数).
【答案】(1)详见解析(2)![]() ,
,
【解析】试题分析:(1)求出![]() 的定义域
的定义域![]() ,
,![]() ,由此利用导数性质和分类讨论思想能求出
,由此利用导数性质和分类讨论思想能求出![]() 的单调区间.
的单调区间.
(2)推导出![]() ,令
,令![]() ,
,![]() ,则
,则![]() 恒成立,由此能求出
恒成立,由此能求出![]() 的取值范围
的取值范围
试题解析:(1)![]() (其中
(其中![]() 是实数),
是实数),
![]() 的定义域
的定义域![]() ,
,![]() ,
,
令![]() ,
,![]() =
=![]() -16,对称轴
-16,对称轴![]() ,
,![]() ,
,
当![]() =
=![]() -16
-16![]() 0,即-4
0,即-4![]() 时,
时,![]() ,
,
![]() 函数
函数![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,
,无单调递减区间,
当![]() =
=![]() -16
-16![]() 0,即
0,即![]() 或
或![]()
![]() 若
若![]() ,则
,则![]() 恒成立,
恒成立,
![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间。
,无单调递减区间。
![]() 若
若![]() 4,令
4,令![]() ,得
,得
![]() =
=![]() ,
,![]() =
=![]() ,
,
当![]() (0,
(0,![]() )
)![]() (
(![]() ,+
,+![]() 时,
时,![]() 当
当![]() (
(![]() )时,
)时,![]()
![]() 的单调递增区间为(0,
的单调递增区间为(0,![]() ),(
),(![]() ),单调递减区间为(
),单调递减区间为(![]() )
)
综上所述当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,无单调递减区间,
,无单调递减区间,
当![]() 时,
时,![]() 的单调递增区间为(0,
的单调递增区间为(0,![]() )和(
)和(![]() ),单调递减区间为(
),单调递减区间为(![]() )
)
(2)由(1)知,若![]() 有两个极值点,则
有两个极值点,则![]() 4,且
4,且![]() ,
,![]() ,
,![]() 又
又![]() ,
,![]() ,
,![]() ,
,![]() ,
,
又![]() ,解得
,解得![]() ,
,
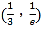
令![]() ,
,![]() 则
则![]() 恒成立
恒成立
![]() 在
在![]() 单调递减,
单调递减,![]() ,
,
即![]()
故![]() 的取值范围为
的取值范围为![]()


科目:高中数学 来源: 题型:
【题目】一组数据中的每一个数据都乘以2,再减去80,得到一组新数据,若求得新的数据的平均数是1.2,方差是4.4,则原来数据的平均数和方差分别是( )
A.40.6,1.1B.48.8,4.4C.81.2,44.4D.78.8,75.6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且左焦点与抛物线
,且左焦点与抛物线![]() 的焦点重合。
的焦点重合。
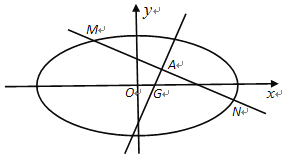
(1)求椭圆的标准方程;
(2)若直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,线段
,线段![]() 的中点记为
的中点记为![]() ,且线段
,且线段![]() 的垂直平分线过定点
的垂直平分线过定点![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子里装有大小均匀的![]() 个小球,其中有红色球
个小球,其中有红色球![]() 个,编号分别为
个,编号分别为![]() ;白色球
;白色球![]() 个, 编号分别为
个, 编号分别为![]() , 从盒子中任取
, 从盒子中任取![]() 个小球(假设取到任何—个小球的可能性相同).
个小球(假设取到任何—个小球的可能性相同).
(1)求取出的![]() 个小球中,含有编号为
个小球中,含有编号为![]() 的小球的概率;
的小球的概率;
(2)在取出的![]() 个小球中, 小球编号的最大值设为
个小球中, 小球编号的最大值设为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 均为真命题,则命题
均为真命题,则命题![]() 为真命题
为真命题
B. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ”
”
C. 在![]() ,“
,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D. 命题![]() “
“![]() ”的否定为
”的否定为![]() “
“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点![]() 处下上至
处下上至![]() 处有两种路径.一种是从
处有两种路径.一种是从![]() 沿直线步行到
沿直线步行到![]() ,另一种是先从
,另一种是先从![]() 沿索道乘缆车到
沿索道乘缆车到![]() ,然后从
,然后从![]() 沿直线步行到
沿直线步行到![]() .现有甲、乙两位游客从
.现有甲、乙两位游客从![]() 处下山,甲沿
处下山,甲沿![]() 匀速步行,速度为
匀速步行,速度为![]() .在甲出发
.在甲出发![]() 后,乙从
后,乙从![]() 乘缆车到
乘缆车到![]() ,在
,在![]() 处停留
处停留![]() 后,再从
后,再从![]() 匀速步行到
匀速步行到![]() ,假设缆车匀速直线运动的速度为
,假设缆车匀速直线运动的速度为![]() ,山路
,山路![]() 长为1260
长为1260![]() ,经测量
,经测量![]() ,
,![]() .
.
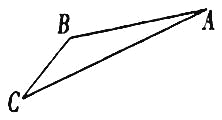
(1)求索道![]() 的长;
的长;
(2)问:乙出发多少![]() 后,乙在缆车上与甲的距离最短?
后,乙在缆车上与甲的距离最短?
(3)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() ,乙步行的速度应控制在什么范围内?
,乙步行的速度应控制在什么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com