
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
2
| ||
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 49 |
| 12 |
| 1 |
| 3 |
| 4 |
| 3 |


科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| |ax-2|+|ax-a|-2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.y=cos2x,x∈R | B.y=log2|x|,x∈R且x≠0) |
C.y=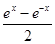 ,x∈R ,x∈R | D.y=x3+1,x∈R |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2-少 x2 的定义域为E,值域为F.(少)若E={少,2},判断实数λ=lg22+lg2lg5+lg5-少6-
|