练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知实数且，函数在上是减函数，则的取值范围为 ，

    此时函数，则，，的大小关系为 ．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2016届湖南省长沙市高三第一次月考文科数学试卷（解析版） 题型：解答题

    定义在上的函数满足：对，都有；当时，，给出如下结论：其中所有正确结论的序号是： ．

    ①对，有；

    ②函数的值域为；

    ③存在，使得；

    ④函数在区间单调递减的充分条件是“存在，使得”．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年广东省普宁市华美实验学校高一上学期期中数学试卷（解析版） 题型：解答题

    已知二次函数y＝f（x）满足f（－2）＝f（4）＝－16，且f（x）最大值为2．

    （1）求函数y＝f（x）的解析式．

    （2）求函数y＝f（x）在[t，t＋1]（t＞0）上的最大值．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年湖北省武汉市高二上学期期中考试数学试卷（解析版） 题型：解答题

    若直线：与直线：平行，求的值．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年河北省高一上学期期中考试理科数学试卷（解析版） 题型：填空题

    计算结果是 ．

    查看答案和解析>>

    科目：高中数学 来源：2016届浙江省绍兴市高三上学期期中理科数学试卷（解析版） 题型：填空题

    设，满足约束条件，若目标函数（，）的最大值为，则的最小值为 ．

    查看答案和解析>>

    科目：高中数学 来源：2016届山西省高三10月月考文科数学试卷（解析版） 题型：选择题

    下列命题中的说法正确的是

    A．若向量，则存在唯一的实数使得；

    B．命题“若，则”的否命题为“若，则”；

    C．命题“，使得”的否定是：“，均有”；

    D．“且”是“”的不充分也不必要条件；

    查看答案和解析>>

    科目：高中数学 来源：2016届江苏省高三上学期周练数学试卷（解析版） 题型：解答题

    已知等比数列的首项，公比，数列前n项和记为，前n项积记为．

    （1）证明：；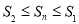

    （2）求n为何值时，取得最大值；

    （3）证明：若数列中的任意相邻三项按从小到大排列，则总可以使其成等差数列；若所有这些等差数列的公差按从大到小的顺序依次记为，则数列为等比数列．

    查看答案和解析>>

    科目：高中数学 来源：2015-2016学年吉林省高一上期中文科数学试卷（解析版） 题型：选择题

    下列不等式正确的是（ ）

    A．

    B．

    C．

    D．

    查看答案和解析>>

    同步练习册答案