
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
分析 根据双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,确定双曲线的顶点与焦点,再根据双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,确定双曲线的渐近线,从而求出椭圆的离心率.
解答 解:∵双曲线的顶点与焦点分别是椭圆$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0)的焦点与顶点,
∴双曲线的顶点是(0,±$\sqrt{{a}^{2}-{b}^{2}}$),焦点是(0,±a),
设双曲线方程为$\frac{{y}^{2}}{{m}^{2}}-\frac{{x}^{2}}{{n}^{2}}=1$(m>0,n>0),
∴双曲线的渐近线方程为y=±$\frac{n}{m}$x,
∵m=$\sqrt{{a}^{2}-{b}^{2}}$,n2=a2-m2=b2,
∴n=b,
∵双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,
∴双曲线的渐近线方程为y=±x,
∴m=n,
∴a2-b2=b2,
∴c2=a2-c2,
∴a2=2c2,
∴a=$\sqrt{2}$c
∴e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题以椭圆方程为载体,考查双曲线的几何性质,考查椭圆的离心率,正确运用几何量的关系是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
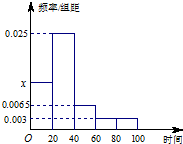 某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)
某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4] | B. | (0,1] | C. | [-1,1] | D. | (4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com