
 某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)
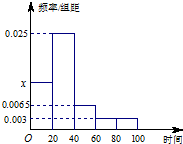
某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟) 分析 由题意,可由直方图中各个小矩形的面积和为1求出x值.根据直方图求平均值的公式,各个小矩形的面积乘以相应组距的中点的值,将它们相加即可得到平均值
解答  解:解:由直方图可得(x+0.025+0.0065+0.003×2)×20=1.所以x=0.0125.
解:解:由直方图可得(x+0.025+0.0065+0.003×2)×20=1.所以x=0.0125.
该校学生上学所需时间的均值估计为:
10×20×0.0125+30×20×0.025+50×20×0.0065+70×20×0.003+90×20×0.003=33.6分钟.
故该校新生上学所需时间的平均值为33.6分
故答案:33.6.
点评 本题考查频率分布直方图,解题的关键是理解直方图中各个小矩形的面积的意义及各个小矩形的面积和为1,本题考查了识图的能力


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{13}{6}$ | C. | $\frac{7}{3}$ | D. | $\frac{15}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
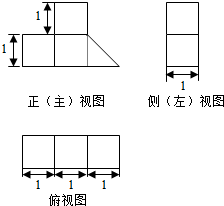
| A. | $\frac{7}{3}$ m3 | B. | $\frac{9}{2}$ m3 | C. | $\frac{9}{4}$ m3 | D. | $\frac{7}{2}$ m3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
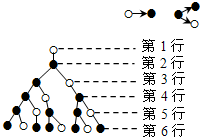 分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照
分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com