
分析 设双曲线E的半焦距为c,根据离心率为$\frac{3\sqrt{5}}{5}$,双曲线方程,即可求实数a的值,设点H(x,y),且过点P($\frac{5}{3}$,1)的直线l与双曲线E的右支交于不同两点M(x1,y1),N(x2,y2),则y12=$\frac{4}{5}$(x12-5),y22=$\frac{4}{5}$(x22-5),设$\frac{PM}{PN}$=$\frac{MH}{HN}$=λ,求出坐标之间的关系,化简可得点H恒在定直线4x-3y-12=0上.
解答 证明:设双曲线E的半焦距为c,
由题意可得$\left\{\begin{array}{l}{\frac{c}{a}=\frac{3\sqrt{5}}{5}}\\{{c}^{2}={a}^{2}+4}\end{array}\right.$,解得a=$\sqrt{5}$.
∴双曲线方程为$\frac{{x}^{2}}{5}-\frac{{y}^{2}}{4}=1$,直线x=$\frac{5}{3}$,点F2(3,0).
设设点H(x,y),点P($\frac{5}{3}$,1)的直线l与双曲线E的右支交于不同两点M(x1,y1),N(x2,y2),则
y12=$\frac{4}{5}$(x12-5),y22=$\frac{4}{5}$(x22-5).
设$\frac{PM}{PN}$=$\frac{MH}{HN}$=λ,则(x1-$\frac{5}{3}$,y1-1)=λ(x2-$\frac{5}{3}$,y2-1),(x-x1,y-y1)=λ(x2-x,y2-y),
∴x1-λx2=$\frac{5}{3}$(1-λ)①,y1-λy2=1-λ②,x1+λx2=x(1-λ)③,y1+λy2=y(1+λ)④,
由①×③得x12-λ2x22=$\frac{5}{3}$(1-λ2)x⑤,②×④得y12-λy22=(1-λ2)y⑥,
将y12=$\frac{4}{5}$(x12-5),y22=$\frac{4}{5}$(x22-5)代入⑥,得y=$\frac{4}{5}×\frac{{{x}_{1}}^{2}-{λ}^{2}{{x}_{2}}^{2}}{1-{λ}^{2}}$-4 ⑦
将⑤代入⑦,得y=$\frac{4}{3}$x-4.
∴点H恒在定直线4x-3y-12=0上
点评 本小题主要考查直线的斜率、双曲线的方程、直线与圆锥曲线的位置关系等知识,考查数形结合、化归与转化、函数与方程的数学思想方法,以及推理论证能力和运算求解能力.


科目:高中数学 来源: 题型:填空题
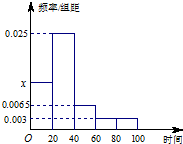 某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)
某学校随机抽取100名学生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中,上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].则该校学生上学所需时间的均值估计为33.6.(精确到1分钟)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a2015=1,S2015=2 | B. | a2015=-3,S2015=2 | ||
| C. | a2015=-1,S2015=2 | D. | a2015=3,S2015=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,4] | B. | (0,1] | C. | [-1,1] | D. | (4,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com