
| A. | $\frac{2}{5}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
分析 设合格饮料为1,2,3,4,不合格饮料为5,6.利用列举法列出从6听中选2听共有15种方法,有1听不合格的有8种,有2听不合格的有1种,最后利用概率公式即可求出所求概率
解答 解:设合格饮料为1,2,3,4,不合格饮料为5,6
则6听中选2听共有(1,2)、(1,3)、(1,4)(1,5)、(1,6)、(2,3)、(2,4)、
(2,5)、(2,6)、(3,4)、(3,5)、(3,6)、(4,5)、(4,6)、(5,6)共15种,
有1听不合格的有(1,5)、(1,6)、(2,5)、(2,6)、(3,5)、(3,6)、(4,5)、(4,6)共8种;
有2听不合格的有(5,6)共1种,
故所求事件的概率为P=$\frac{8+1}{15}$=$\frac{3}{5}$.
故选:C.
点评 本题考查等可能事件的概率计算,体现了分类讨论的数学思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
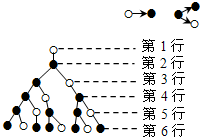 分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照
分形几何学是美籍法国数学家伯努瓦•曼德尔布罗(BenoitBMandelbrot)在20世纪70年代创立的一门新学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{9}{10}$,$\sqrt{2}$)∪(-1,-$\frac{9}{10}$) | B. | (-1,$\sqrt{2}$] | C. | (-1,-$\frac{9}{10}$) | D. | (-$\frac{9}{10}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{1}{2}\sqrt{5}$ | C. | $\sqrt{5}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com