Question

8．若某几何体的三视图是如图所示的三个直角三角形，则该几何体的外接球的表面积为50π．

Answer 1

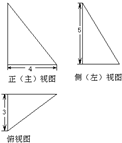
分析 几何体复原为底面是直角三角形，一条侧棱垂直底面直角顶点的三棱锥，扩展为长方体，长方体的对角线的长，就是外接球的直径，然后求其的表面积．

解答 解：由三视图复原几何体，几何体是底面是直角三角形，
一条侧棱垂直底面直角顶点的三棱锥；扩展为长方体，
其外接与球，它的对角线的长为球的直径，
得长方体的体对角线的长为$\sqrt{{3}^{2}+{4}^{2}+{5}^{2}}$=5$\sqrt{2}$，
∴长方体的外接球的半径为$\frac{5\sqrt{2}}{2}$，
∴球的表面积为4π$（\frac{5\sqrt{2}}{2}）^{2}$=50π，
故答案为：50π．

点评 本题考查三视图，几何体的外接球的表面积，考查空间想象能力，计算能力，是基础题．