
分析 (1)根据题意由X=3且甲获得冠军可得设A1:甲恰胜2局;A2:和2局;列式求解.
(2)随机变量X的所有可能和每种可能的概率,得分布列和期望.
解答 解:(1)设A1:甲恰胜2局;A2:和2局;
则P(A)=P(A1∪A2)=P(A1)+P(A2)=$({C}_{2}^{1}×\frac{1}{3}×\frac{2}{3})×\frac{1}{3}$$+({C}_{2}^{1}×\frac{1}{3}×\frac{2}{3})×\frac{1}{3}=\frac{8}{27}$
(2)X可能取得值为2,3,4
P(X=2)=$3×\frac{1}{3}×\frac{1}{3}=\frac{1}{3}$;
P(X=3)=3×$[{C}_{2}^{1}×\frac{1}{3}×\frac{2}{3}]×\frac{1}{3}=\frac{4}{9}$;
P(X=4)=${A}_{3}^{3}(\frac{1}{3})^{3}=\frac{2}{9}$
分布列为:
| X | 2 | 3 | 4 |
| P | $\frac{1}{3}$ | $\frac{4}{9}$ | $\frac{2}{9}$ |
点评 本题主要考查随机变量的分布列和期望,属于中档题型,在高考中经常涉及.


科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{9}{10}$,$\sqrt{2}$)∪(-1,-$\frac{9}{10}$) | B. | (-1,$\sqrt{2}$] | C. | (-1,-$\frac{9}{10}$) | D. | (-$\frac{9}{10}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有且只有一个 | B. | 有四个 | C. | 有无数个 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
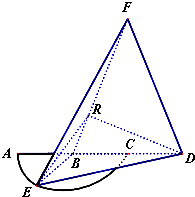 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
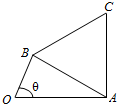 已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.
已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com