
| A. | 等腰直角三角形 | B. | 直角三角形 | C. | 等腰三角形 | D. | 等边三角形 |
分析 设出P点坐标,对抛物线方程进行求导表示出PN和PT的斜率,则直线PN的方程可得,令x=0,求得N点坐标,进而可表示出|NF|,由抛物线定义可知|PF|,推断出|PF|=|NF|,把x=0代入直线l的方程求得T点坐标,表示出
|TF|,进而可知|NF|=|TF|=|PF|.
解答 解:由x2=4y,得焦点F(0,1),设P(x0,$\frac{1}{4}{{x}_{0}}^{2}$),
由y′=$\frac{1}{2}$x,知kl=${y}^{′}{|}_{x={x}_{0}}$=$\frac{1}{2}{x}_{0}$,则${k}_{PN}=-\frac{2}{{x}_{0}}$,
直线PN的方程为:y-$\frac{1}{4}{{x}_{0}}^{2}$=-$\frac{2}{{x}_{0}}$(x-x0),
令x=0,得N(0,$\frac{{{x}_{0}}^{2}}{4}+2$),点F(0,1),
则|NF|=$\frac{{{x}_{0}}^{2}}{4}+1$.
由抛物线定义知|PF|=$\frac{{{x}_{0}}^{2}}{4}$-(-1)=$\frac{{{x}_{0}}^{2}}{4}$+1,
即|PF|=|NF|,
直线l的方程为y-$\frac{{{x}_{0}}^{2}}{4}$=$\frac{{x}_{0}}{2}$(x-x0),
令x=0,得到${y}_{T}=-\frac{{{x}_{0}}^{2}}{4}$,∴|TF|=$\frac{{{x}_{0}}^{2}}{4}$+1,
故|NF|=|TF|=|PF|.
∴△PNF为等腰三角形.
故选:C.
点评 本题主要考查了抛物线的定义及性质的运用.考查了学生综合分析问题的能力,属中档题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,2] | B. | [-1,0) | C. | [2,4) | D. | [1,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{8}{13}$ | B. | $\frac{17}{28}$ | C. | $\frac{2}{3}$ | D. | $\frac{18}{29}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 671 | B. | 672 | C. | 1342 | D. | 1344 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
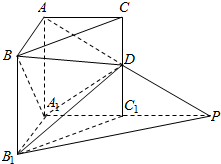 如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.
如图所示,在直三棱柱ABC-A1B1B1中,∠BAC=90°,AB=AC=AA1=1,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 4 | D. | $2\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com