
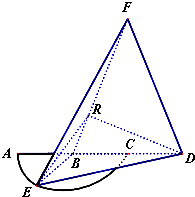
 如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.
如图,弧$\widehat{AEC}$是半径为a的半圆,AC为直径,点E为弧$\widehat{AC}$的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FB=FD=$\sqrt{5}$a,FE=$\sqrt{6}$a.分析 (1)欲证EB⊥FD,而FD?平面BFD,可先证BE⊥平面BFD,根据直线与平面垂直的判定定理可知只需证BE与平面BFD内两相交直线垂直,而BE⊥AC,根据线面垂直的性质可知FC⊥BE,又FC、AC?平面BFD,FC∩AC=C,满足定理所需条件;
(2)RD最短时,RD⊥FB,过R做RH⊥平面BDF,∠REH即为RE和平面BDE所成的角,求出$RH=\frac{4}{5}a,RE=\frac{3}{{\sqrt{5}}}a$,所以$sinREH=\frac{{4\sqrt{5}}}{15}$.
解答  (1)证明:∵点E为弧AC的中点
(1)证明:∵点E为弧AC的中点
∴∠ABE=$\frac{π}{2}$,即BE⊥AC
又∵FC⊥平面BED,BE?平面BED
∴FC⊥BE
又∵FC、AC?平面BFD,FC∩AC=C
∴BE⊥平面BFD而FD?平面BFD
∴EB⊥FD;
(2)解:RD最短时,RD⊥FB,过R做RH⊥平面BDE,则∠REH即为RE和平面BDE所成的角,
∵$RH=\frac{4}{5}a,RE=\frac{3}{{\sqrt{5}}}a$,∴$sinREH=\frac{{4\sqrt{5}}}{15}$.
点评 本题考查线面垂直的判定与性质,考查线面角,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)为偶函数且最小正周期为π | B. | f(x)为奇函数且最小正周期为π | ||
| C. | f(x)为偶函数且最小正周期为2π | D. | f(x)为奇函数且最小正周期为2π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题p∨q是假命题 | B. | 命题p∧q是真命题 | ||
| C. | 命题p∧(¬q)是真命题 | D. | 命题p∨(¬q)是假命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com