
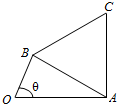
 ��֪����f��x��=sin��x��0���أ�2�������䣬[0��$\frac{��}{3}$]�ϵ���������������[$\frac{��}{3}$��$\frac{2��}{3}$]�����ݼ�����ͼ���ı���OACB�У�a��b��cΪ��ABC���ڽ�A��B��C�ĶԱߣ�������$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4��}{3}-cosB-cosC}{cosA}$��
��֪����f��x��=sin��x��0���أ�2�������䣬[0��$\frac{��}{3}$]�ϵ���������������[$\frac{��}{3}$��$\frac{2��}{3}$]�����ݼ�����ͼ���ı���OACB�У�a��b��cΪ��ABC���ڽ�A��B��C�ĶԱߣ�������$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4��}{3}-cosB-cosC}{cosA}$������ ��1��������֪ $\frac{2��}{��}$=$\frac{4��}{3}$����֮�ɵæأ�������֪��������ɵ�sinC+sinB=2sinA���������Ҷ����ɵ�b+c=2a��
��2���������ͣ�1���Ľ��ۿɵá�ABCΪ�ȱ������Σ��ɵ�SOACB=S��OAB+S��ABC=$\frac{1}{2}$OA•OBsin��+$\frac{\sqrt{3}}{4}$AB2���ɻ���Ϊ2sin����-$\frac{��}{3}$��+$\frac{5\sqrt{3}}{4}$���ɦȵķ�Χ�ɵý��ۣ�
��� ֤������1��������֪��$\frac{2��}{��}$=$\frac{4��}{3}$����æ�=$\frac{3}{2}$ ����2�֣�
��$\frac{sinB-sinC}{sinA}$=$\frac{\frac{4��}{3}-cosA•cosC}{cosA}$��
��sinBcosA+sinCcosA=2sinA-cosBsinA-cosCsinA��
��sinBcosA+cosBsinA+sinCcosA+cosCsinA=2sinA��
��sin��A+B��+sin��A+C��=2sinA����4�֣�
��sinC+sinB=2sinA��
��b+c=2a����6�֣�
�⣺��2����Ϊb+c=2a��b=c������a=b=c�����ԡ�ABCΪ�ȱ������Σ�
SOACB=S��OAB+S��ABC=$\frac{1}{2}$OA•OBsin��+$\frac{\sqrt{3}}{4}$AB2������8�֣�
=sin��+$\frac{\sqrt{3}}{4}$��OA2+OB2-2OA•OBcos�ȣ�����9�֣�
=sin��-$\sqrt{3}$cos��+$\frac{5\sqrt{3}}{4}$=2sin����-$\frac{��}{3}$��+$\frac{5\sqrt{3}}{4}$������10�֣�
�ߦȡʣ�0���У������-$\frac{��}{3}$�ʣ�-$\frac{��}{3}$��$\frac{2��}{3}$����
���ҽ�����-$\frac{��}{3}$=$\frac{��}{2}$������=$\frac{5��}{6}$ʱȡ���ֵ��SOACB�����ֵΪ2+$\frac{5\sqrt{3}}{4}$����12�֣�
���� ���⿼�����Ǻ��������Ǻ�����ʽ���漰���Ҷ����������ε���������е��⣮


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{3}{4}+\frac{1}{4}$i | B�� | -$\frac{1}{4}+\frac{3}{4}$i | C�� | -1+$\frac{1}{2}$i | D�� | -1-$\frac{1}{2}$i |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\sqrt{3}$ | C�� | 4 | D�� | $2\sqrt{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | -3 | C�� | 3 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com