
分析 首先将原式变形为cos$\frac{2π}{7}$cos$\frac{4π}{7}$cos(π-$\frac{π}{7}$)的形式,观察角度关系恰好是二倍角关系,所以分子、分母同时乘8sin$\frac{π}{7}$,3次运用正弦的二倍角公式化简求值.
解答 解:原式=cos$\frac{2π}{7}$cos$\frac{4π}{7}$cos(π-$\frac{π}{7}$)=-$\frac{8sin\frac{π}{7}cos\frac{π}{7}cos\frac{2π}{7}cos\frac{4π}{7}}{8sin\frac{π}{7}}$=-$\frac{4sin\frac{2π}{7}cos\frac{2π}{7}cos\frac{4π}{7}}{8sin\frac{π}{7}}$=-$\frac{2sin\frac{4π}{7}cos\frac{4π}{7}}{8sin\frac{π}{7}}$=-$\frac{sin\frac{8π}{7}}{8sin\frac{π}{7}}$=-$\frac{-sin\frac{π}{7}}{8sin\frac{π}{7}}$=$\frac{1}{8}$;
故答案为:$\frac{1}{8}$.
点评 本题考查了三角函数式的化简求值;关键是发现角度的关系,巧配二倍角公式.


 计算高手系列答案
计算高手系列答案科目:高中数学 来源: 题型:填空题
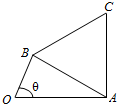 已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.
已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | k>-$\frac{b}{a}$ | B. | k<$\frac{b}{a}$ | C. | k>$\frac{b}{a}$或k<-$\frac{b}{a}$ | D. | -$\frac{b}{a}$<k<$\frac{b}{a}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,5] | B. | [-2,2] | C. | [-2,5] | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com