
分析 ①画出y=m和y=|lnx|的图象,求出切线的斜率,求出交点的坐标M,N,即可得到MN的长,即可判断①;
②通过图象观察分析,两切线垂直,即可判断②;
③求出P的坐标,再求PQ长,即可判断③;
④由零点的定义,求出AO的长,运用函数的性质,即可判断④.
解答 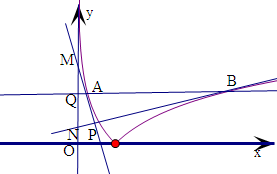 解:对于①,作出函数的图象,由|lnx1|=|lnx2|,可得,-lnx1=lnx2,
解:对于①,作出函数的图象,由|lnx1|=|lnx2|,可得,-lnx1=lnx2,
所以x1x2=1,且0<x1<1,x2>1,故A(x1,-lnx1)B(x2,lnx2),
在A点处的切线斜率为-$\frac{1}{{x}_{1}}$,在B点处的切线斜率为:$\frac{1}{{x}_{2}}$,
则设M(0,s),N(0,n),
则有$\frac{s+{lnx}_{1}}{-{x}_{1}}$=-$\frac{1}{{x}_{1}}$,解得,s=1-lnx1,
由$\frac{n-{lnx}_{2}}{-{x}_{2}}$=$\frac{1}{{x}_{2}}$,解得,n=lnx2-1,
则有|MN|=1-lnx1-(lnx2-1)=2-ln(x1x2)=2,故①正确;
对于②,若△PAB为等腰三角形,即PA=PB,或PA=AB,或PB=AB,
若PA=PB,则P在AB的中垂线上,不可能;若PA=AB,易得P的横坐标小于1,不成立;
若PB=AB,则由于-$\frac{1}{{x}_{1}}$•$\frac{1}{{x}_{2}}$=-1,即有PA⊥BP,则不成立,故②错误;
对于③,Q(0,m),由y+lnx1=1-$\frac{1}{{x}_{1}}$x和y-lnx2=$\frac{x}{{x}_{2}}$-1,x1x2=1,
解得交点P($\frac{2{x}_{1}}{1+{x}_{1}^{2}}$,1-lnx1-$\frac{2}{1+{x}_{1}^{2}}$),由于m=lnx2=-lnx1,
则有|PQ|=$\sqrt{(\frac{2{x}_{1}}{1+{x}_{1}^{2}})^{2}+(\frac{{{x}_{1}}^{2}-1}{1+{x}_{1}^{2}})^{2}}$=1.故③正确;
对于④,当x1是函数g(x)=x2+lnx的零点时,即有x12+lnx1=0,
|$\overrightarrow{AO}$|=$\sqrt{{x}_{1}^{2}+({lnx}_{1})^{2}}$,则|$\overrightarrow{AO}$|2=${x}_{1}^{2}+{({lnx}_{1})}^{2}$=x12+x14,
故不存在x1∈(0,1),$|{\overrightarrow{AO}}$|(O为坐标原点)取最小值,
故④不正确.
故答案为:①③.
点评 本题考查导数的几何意义,着重考查曲线在该点处的切线的斜率,两点的距离和点到直线的距离公式及函数的最值的求法,考查转化思想与分析运算、判断求解能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 有且只有一个 | B. | 有四个 | C. | 有无数个 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{5}{3}$ | C. | $\frac{8}{5}$ | D. | $\frac{12}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | [0,1] | C. | [-1,2] | D. | [1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
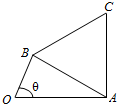 已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.
已知函数f(x)=sinωx(0<ω<2)在区间,[0,$\frac{π}{3}$]上单调递增,在区间[$\frac{π}{3}$,$\frac{2π}{3}$]单调递减;如图,四边形OACB中,a,b,c为△ABC的内角A,B,C的对边,且满足$\frac{sinB+sinC}{sinA}$=$\frac{\frac{4ω}{3}-cosB-cosC}{cosA}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com