
| A. | (0,$\frac{1}{3}$) | B. | ($\frac{1}{3}$,1) | C. | (0,$\frac{2}{3}$) | D. | ($\frac{2}{3}$,1) |
分析 作出图形,则易知|AF2|=a+c,|BF2|=$\frac{{a}^{2}-{c}^{2}}{a}$,再由∠BAF2是直线的倾斜角,易得k=tan∠BAF2,然后通过0<k<$\frac{1}{3}$,分子分母同除a2得0<$\frac{1-{e}^{2}}{1+e}$<$\frac{1}{3}$求解.
解答 解:如图所示:|AF2|=a+c,|BF2|=$\frac{{a}^{2}-{c}^{2}}{a}$,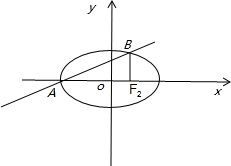
∴k=tan∠BAF2=$\frac{{a}^{2}-{c}^{2}}{a(a+c)}$,
又∵0<k<$\frac{1}{3}$,
∴0<$\frac{{a}^{2}-{c}^{2}}{a(a+c)}$<$\frac{1}{3}$,
∴0<$\frac{1-{e}^{2}}{1+e}$<$\frac{1}{3}$,
∴$\frac{2}{3}$<e<1.
故选:D.
点评 本题考查了椭圆与直线的位置关系及椭圆的几何性质和直线的斜率与倾斜角,难度不大,但需要灵活运用和转化知识.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 4 | D. | $2\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|X≥2} | B. | {x|x>2} | C. | {x|x≤0或x≥2} | D. | {x|0<x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com