
【题目】已知函数![]()
(1)讨论函数![]() 的单凋性;
的单凋性;
(2)若存在![]() 使得对任意的
使得对任意的![]() 不等式
不等式![]() (其中e为自然对数的底数)都成立,求实数
(其中e为自然对数的底数)都成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:
(1)首先求解导函数,然后利用二次函数的性质结合导函数的分子分类讨论函数的单调区间即可;
(2)将问题进行等价转化,构造![]() ,结合函数
,结合函数![]() 的性质求解实数
的性质求解实数![]() 的取值范围即可.
的取值范围即可.
试题解析:
(I)![]()
![]() ,记
,记![]()
(i)当![]() 时,因为
时,因为![]() ,所以
,所以![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(ii)当![]() 时,因为
时,因为![]() ,
,
所以![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
(iii)当![]() 时,由
时,由![]() ,解得
,解得 ,
,
所以函数![]() 在区间
在区间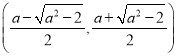 上单调递减,
上单调递减,
在区间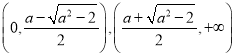 上单调递增.
上单调递增.
(II)由(I)知当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以当![]() 时,函数
时,函数![]() 的最大值是
的最大值是![]() ,对任意的
,对任意的![]() ,
,
都存在![]() ,使得不等式
,使得不等式![]() 成立,
成立,
等价于对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
即对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
记![]() ,由
,由![]() ,
,
![]() ,
,
由![]() 得
得![]() 或
或![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
①当![]() 时,
时, ![]() ,且
,且![]() 时,
时, ![]() ,
,
![]() 时,
时, ![]() ,所以
,所以![]() ,
,
所以![]() 时,
时, ![]() 恒成立;
恒成立;
②当![]() 时,
时, ![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
此时![]() 单调递增,且
单调递增,且![]() ,
,
所以![]() 时,
时, ![]() 成立;
成立;
③当![]() 时,
时, ![]() ,
, ![]() ,
,
所以存在![]() 使得
使得![]() ,因此
,因此![]() 不恒成立.
不恒成立.
综上, ![]() 的取值范围是
的取值范围是![]() .
.
另解(II)由(Ⅰ)知,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() 时,函数
时,函数![]() 的最大值是
的最大值是![]() ,
,
对任意的![]() ,都存在
,都存在![]() ,
,
使得不等式![]() 成立,
成立,
等价于对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
即对任意的![]() ,不等式
,不等式![]() 都成立,
都成立,
记![]() ,
,
由![]() ,且
,且![]()
∴对任意的![]() ,不等式
,不等式![]() 都成立的必要条件为
都成立的必要条件为![]()
又![]() ,
,
由![]() 得
得![]() 或
或![]()
因为![]() ,所以
,所以![]() ,
,
当![]() 时,
时, ![]() ,且
,且![]() 时,
时, ![]() ,
,
![]() 时,
时, ![]() ,所以
,所以![]() ,
,
所以![]() 时,
时, ![]() 恒成立;
恒成立;
②当![]() 时,
时, ![]() ,因为
,因为![]() ,所以
,所以![]() ,
,
此时![]() 单调递增,且
单调递增,且![]() ,
,
所以![]() 时,
时, ![]() 成立.
成立.
综上, ![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴非负半轴为极轴建立极坐标系,直线
轴非负半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及直线
的极坐标方程及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过点![]() 作抛物线
作抛物线![]() 的两条切线, 切点分别为
的两条切线, 切点分别为![]() ,
, ![]() .
.
(1) 证明: ![]() 为定值;
为定值;
(2) 记△![]() 的外接圆的圆心为点
的外接圆的圆心为点![]() , 点
, 点![]() 是抛物线
是抛物线![]() 的焦点, 对任意实数
的焦点, 对任意实数![]() , 试判断以
, 试判断以![]() 为直径的圆是否恒过点
为直径的圆是否恒过点![]() ? 并说明理由.
? 并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
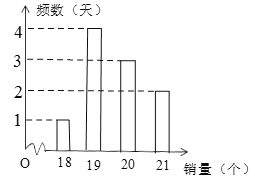
【题目】某商场对某一商品搞活动,已知该商品每一个的进价为3元,销售价为8元,每天售出的第20个及之后的半价出售.该商场统计了近10天的这种商品销量,如图所示:设![]() 为每天商品的销量,
为每天商品的销量,![]() 为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
为该商场每天销售这种商品的的利润.从日利润不少于96元的几天里任选2天,则选出的这2天日利润都是97元的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解本市居民的生活成本,甲、乙、丙三名同学利用假期分别对三个社区进行了“家庭每月日常消费额”的调查.他们将调查所得到的数据分别绘制成频率分布直方图(如图所示),记甲、乙、丙所调查数据的标准差分别为s1、s2、s3,则它们的大小关系为__________.(用“>”连接)
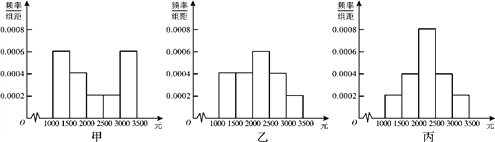
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com