
【题目】已知向量 ![]() ,且
,且 ![]() ,
,
(1)求 ![]() 的取值范围;
的取值范围;
(2)求证 ![]() ;
;
(3)求函数 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:∵ ![]() =sinxcosx+sinxcosx=2sinxcosx=sin2x
=sinxcosx+sinxcosx=2sinxcosx=sin2x
∵x∈[0, ![]() ],
],
∴2x∈[0,π]
∴ ![]() ∈[0,1]
∈[0,1]
(2)解:证明:∵=(cos+sinx,sinx+cosx)
∴| ![]() |=
|= ![]()
= ![]()
∵x∈[0, ![]() ],
],
∴x+ ![]() ∈[
∈[ ![]() ,
, ![]() ],
],
∴sin(x+ ![]() )>0,
)>0,
∴ ![]() =2sin(x+
=2sin(x+ ![]() ),
),
∴| ![]() +
+ ![]() |=2sin(x+
|=2sin(x+ ![]() ).
).
(3)解:∵x∈[0, ![]() ],
],
∴x+ ![]() ∈[
∈[ ![]() ,
, ![]() ]
]
∴f(x)= ![]()
= ![]()
=2sinxcosx﹣2(sinx+cosx)
解法1:令t=sinx+cosx
∴ ![]()
∴y=t2﹣1﹣2t
=(t﹣1)2﹣2
∴y∈ ![]() ,
,
解法2:f(x)=sin2x﹣2 ![]()
= ![]()
= ![]() ﹣1
﹣1
∵ ![]() ≤1
≤1
∴f(x)∈[﹣2, ![]() ]
]
【解析】(1)利用向量的坐标运算公式可求得 ![]() =sin2x,又x∈[0,
=sin2x,又x∈[0, ![]() ],从而可求
],从而可求 ![]() 的取值范围;(2)由
的取值范围;(2)由 ![]() =(cos+sinx,sinx+cosx)由向量模的概念结合辅助角公式即可证得|
=(cos+sinx,sinx+cosx)由向量模的概念结合辅助角公式即可证得| ![]() |=2sin(x+
|=2sin(x+ ![]() ).(3)将
).(3)将 ![]() 化简为:f(x)═2sinxcosx﹣2(sinx+cosx),解法1:令t=sinx+cosx,sinxcosx=
化简为:f(x)═2sinxcosx﹣2(sinx+cosx),解法1:令t=sinx+cosx,sinxcosx= ![]() (1≤t≤
(1≤t≤ ![]() ),y=t2﹣1﹣2t=(t﹣1)2﹣2取值范围可求. 解法2:f(x)=sin2x﹣2
),y=t2﹣1﹣2t=(t﹣1)2﹣2取值范围可求. 解法2:f(x)=sin2x﹣2 ![]() sin(x+
sin(x+ ![]() )=
)= ![]() ﹣1,求得sin(x+
﹣1,求得sin(x+ ![]() )的范围即可.
)的范围即可.
【考点精析】认真审题,首先需要了解二次函数在闭区间上的最值(当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() ).
).


 习题精选系列答案
习题精选系列答案科目:高中数学 来源: 题型:
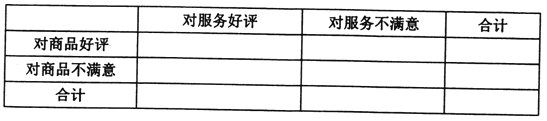
【题目】现如今,“网购”一词不再新鲜,越来越多的人已经接受并喜欢了这种购物方式,但随之也出现了商品质量不能保证与信誉不好等问题,因此,相关管理部门制定了针对商品质量与服务的评价体系,现从评价系统中选出成功交易200例,并对其评价进行统计:对商品的好评率为0.6,对服务的好评率为0.75,其中对商品和服务都做出好评的交易为80次.
(1)依据题中的数据完成下表,并通过计算说明,能否有99.9%的把握认为“商品好评与服务好评”有关;
(2)若将频率视为概率,某人在该购物平台上进行了5次购物,设对商品和服务全好评的次数为随机变量![]() ,求
,求![]() 的分布列(概率用算式表示)、数学期望和方差.
的分布列(概率用算式表示)、数学期望和方差.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(a>0且a≠1)是定义在R上的奇函数. (Ⅰ) 求实数a的值;
(Ⅱ) 证明函数f(x)在R上是增函数;
(Ⅲ)当x∈[1,+∞)时,mf(x)≤2x﹣2恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 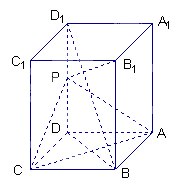
(1)求证:直线BD1∥平面PAC;
(2)求证:直线PB1⊥平面PAC.
(3)求三棱锥B﹣PAC的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() (
(![]() )的焦距为4,左、右焦点分别为
)的焦距为4,左、右焦点分别为![]() 、
、![]() ,且
,且![]() 与抛物线
与抛物线![]() :
: ![]() 的交点所在的直线经过
的交点所在的直线经过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)分别过![]() 、
、![]() 作平行直线
作平行直线![]() 、
、![]() ,若直线
,若直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,与抛物线
两点,与抛物线![]() 无公共点,直线
无公共点,直线![]() 与
与![]() 交于
交于![]() ,
, ![]() 两点,其中点
两点,其中点![]() ,
, ![]() 在
在![]() 轴上方,求四边形
轴上方,求四边形![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 经过点
经过点![]() ,
, ![]() 在点
在点![]() 处的切线交
处的切线交![]() 轴于点
轴于点![]() ,直线
,直线![]() 经过点
经过点![]() 且垂直于
且垂直于![]() 轴.
轴.
(1)求线段![]() 的长;
的长;
(2)设不经过点![]() 和
和![]() 的动直线
的动直线![]() 交
交![]() 于点
于点![]() 和
和![]() ,交
,交![]() 于点
于点![]() ,若直线
,若直线![]() 、
、![]() 、
、![]() 的斜率依次成等差数列,试问:
的斜率依次成等差数列,试问: ![]() 是否过定点?请说明理由.
是否过定点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com