Question

【题目】现如今，“网购”一词不再新鲜，越来越多的人已经接受并喜欢了这种购物方式，但随之也出现了商品质量不能保证与信誉不好等问题，因此，相关管理部门制定了针对商品质量与服务的评价体系，现从评价系统中选出成功交易200例，并对其评价进行统计：对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次.

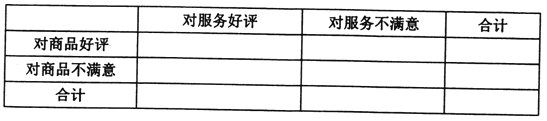
（1）依据题中的数据完成下表，并通过计算说明，能否有99.9%的把握认为“商品好评与服务好评”有关；

（2）若将频率视为概率，某人在该购物平台上进行了5次购物，设对商品和服务全好评的次数为随机变量，求的分布列（概率用算式表示）、数学期望和方差.

Answer 1

【答案】（Ⅰ）有%的把握（Ⅱ），

【解析】试题分析：（1）利用样本乘以商品好评率得到好评人数，用样本乘以服务好评率得到对服务满意人数，由此填写联表，计算出，故有的把握认为“商品好评和服务好评”有关.（2）对商品和服务都好评的概率为， 次购物相当于的独立重复试验，故利用二项分布来计算分布列、期望和方程.

试题解析：

（1） 根据题中条件可得关于商品和服务的列联表：

		对服务好评		对服务不满意		合计
对商品好评
对商品不满意
合计

因此，有%的把握认为“商品好评与服务好评”有关.

（2）由题可得，每次购物时，对商品和服务都好评的概率为

的所有可能的取值为，则～，

所以， ， ，

， ，

分布列为：

由于～，

所以，