等差数列{an}前n项和为Sn.S7+S5=10.a3=5.则S7=( )A．25B．49C．-15D．40 题目和参考答案——青夏教育精英家教网—

15．等差数列{a_n}前n项和为S_n，S₇+S₅=10，a₃=5，则S₇=（　　）

A．

B．

C．

-15

D．

分析利用等差数列的通项公式和前n项和公式列出方程组，求出首项和公差，由此能求出S₇．

解答解：∵等差数列{a_n}前n项和为S_n，S₇+S₅=10，a₃=5，
∴$\left\{\begin{array}{l}{7{a}_{1}+\frac{7×6}{2}d+5{a}_{1}+\frac{5×4}{2}d=10}\\{{a}_{1}+2d=5}\end{array}\right.$，
解得${a}_{1}=\frac{135}{7}$，d=-$\frac{50}{7}$，
∴S₇=$7{a}_{1}+\frac{7×6}{2}d$=$7×\frac{135}{7}+\frac{7×6}{2}×（-\frac{50}{7}）$=-15．
故选：C．

点评本题考查等差数列的性质，考查推理论证能力、运算求解能力，考查函数与方程思想、化归转化思想，是基础题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

5．

如图所示：湖面上甲、乙、丙三艘船沿着同一条直线航行，某一时刻，甲船在最前面的A点处，乙船在中间B点处，丙船在最后面的C点处，且BC：AB=3：1．一架无人机在空中的P点处对它们进行数据测量，在同一时刻测得∠APB=30°，∠BPC=90°．（船只与无人机的大小及其它因素忽略不计）
（1）求此时无人机到甲、丙两船的距离之比；
（2）若此时甲、乙两船相距100米，求无人机到丙船的距离．（精确到1米）

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

6．已知函数$f（x）=a{x^{\frac{3}{2}}}-lnx-\frac{2}{3}$的图象的一条切线为x轴．
（Ⅰ）求实数a的值；
（Ⅱ）令g（x）=|f（x）+f'（x）|，若不相等的两个实数x₁，x₂满足g（x₁）=g（x₂），求证：x₁x₂＜1．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

3．已知△ABC的顶点A（1，0），点B在x轴上移动，|AB|=|AC|，且BC的中点在y轴上．
（Ⅰ）求C点的轨迹Γ的方程；
（Ⅱ）已知轨迹Γ上的不同两点M，N与P（1，2）的连线的斜率之和为2，求证：直线MN过定点．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

10．已知直线ax-2by=2（a＞0，b＞0）过圆x²+y²-4x+2y+1=0的圆心，则$\frac{1}{a}+\frac{1}{b}$的最小值为4．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

20．已知长方体ABCD-A₁B₁C₁D₁中，$A{A_1}=AB=\sqrt{3}$，AD=1，则异面直线B₁C和C₁D所成角的余弦值为（　　）

A．

$\frac{{\sqrt{6}}}{4}$

B．

$\frac{{\sqrt{6}}}{3}$

C．

$\frac{{\sqrt{2}}}{6}$

D．

$\frac{{\sqrt{3}}}{6}$

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

7．若数列{a_n}的前n项和为${S_n}=\frac{2}{3}{n^2}-\frac{1}{3}n$，则数列a_n=$\frac{4}{3}$n-1．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

4．

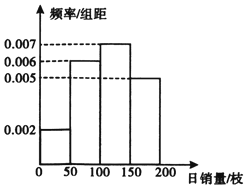某鲜花店根据以往某品种鲜花的销售记录，绘制出日销售量的频率分布直方图，如图所示．将日销售量落入各组区间的频率视为概率，且假设每天的销售量相互独立．
（1）求在未来的连续4天中，有2天的日销售量低于100枝且另外2天不低于150枝的概率；
（2）用ξ表示在未来4天里日销售量不低于100枝的天数，求随机变量ξ的分布列和数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

5．以抛物线Γ的顶点为圆心，$\sqrt{2}$为半径的圆交Γ于A、B两点，且AB=2
（1）建立适当的坐标系，求Γ的方程；
（2）若过点A且与Γ只有一个公共点的直线交Γ的对称轴于点C，点D在线段AB上，直线CD与Γ交于P、Q两点，求证：PC•QD=PD•QC．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学