
 如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)
如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)分析 (1)利用正弦定理,即可求此时无人机到甲、丙两船的距离之比;
(2)若此时甲、乙两船相距100米,由余弦定理求无人机到丙船的距离.
解答 解:(1)在△APB中,由正弦定理,得,$\frac{AP}{sin∠APB}=\frac{AB}{sin∠APB}=\frac{AB}{{\frac{1}{2}}}$,
在△BPC中,由正弦定理,得$\frac{CP}{sin∠CBP}=\frac{BC}{sin∠CPB}=\frac{BC}{1}$,
又$\frac{BC}{AB}=\frac{3}{1}$,sin∠ABP=sin∠CBP,
故$\frac{AP}{CP}=\frac{2}{3}$.即无人机到甲、丙两船的距离之比为$\frac{2}{3}$.
(2)由BC:AB=3:1得AC=400,且∠APC=120°,
由(1),可设AP=2x,则CP=3x,
在△APC中,由余弦定理,得160000=(2x)2+(3x)2-2(2x)(3x)cos120°,
解得$x=\frac{400}{{\sqrt{19}}}=\frac{{400\sqrt{19}}}{19}$,
即无人机到丙船的距离为$CP=3x=\frac{{1200\sqrt{19}}}{19}$≈275米.
点评 本题考查利用数学知识解决实际问题,考查正弦定理、余弦定理的运用,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{6}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 有一个对称中心$({\frac{π}{12},0})$ | B. | 有一条对称轴$x=\frac{π}{6}$ | ||
| C. | 在区间$[{-\frac{π}{12},\frac{5π}{12}}]$上单调递减 | D. | 在区间$[{-\frac{5π}{12},\frac{π}{12}}]$上单调递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
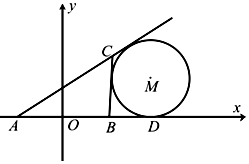 如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
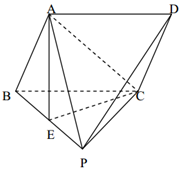 如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.
如图,点P是平行四边形ABCD所在平面外一点,△PBC是等边三角形,点A在平面PBC的正投影E恰好是PB中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com