
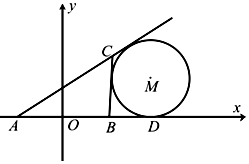
 如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.
如图所示,在△ABC中,AB的中点为O,且OA=1,点D在AB的延长线上,且$BD=\frac{1}{2}AB$.固定边AB,在平面内移动顶点C,使得圆M与边BC,边AC的延长线相切,并始终与AB的延长线相切于点D,记顶点C的轨迹为曲线Γ.以AB所在直线为x轴,O为坐标原点如图所示建立平面直角坐标系.分析 (Ⅰ)确定点C轨迹Γ是以A,B为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点,即可求曲线Γ的方程;
(Ⅱ)可设直线$OE:y=kx,OF:y=-\frac{1}{k}x,E({{x_1},{y_1}}),F({{x_2},{y_2}})$,进而表示面积,即可求△OEF面积的取值范围.
解答 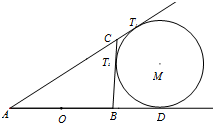 解:(Ⅰ)依题意得AB=2,BD=1,设动圆M与边AC的延长线相切于T1,与边BC相切于T2,则AD=AT1,BD=BT2,CT1=CT2
解:(Ⅰ)依题意得AB=2,BD=1,设动圆M与边AC的延长线相切于T1,与边BC相切于T2,则AD=AT1,BD=BT2,CT1=CT2
所以AD+BD=AT1+BT2=AC+CT1+BT2=AC+CT1+CT2=AC+BC=AB+2BD=4>AB=2…(2分)
所以点C轨迹Γ是以A,B为焦点,长轴长为4的椭圆,且挖去长轴的两个顶点.则曲线Γ的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1({y≠0})$.…(4分)
(Ⅱ)由于曲线Γ要挖去长轴两个顶点,所以直线OE,OF斜率存在且不为0,所以可设直线$OE:y=kx,OF:y=-\frac{1}{k}x,E({{x_1},{y_1}}),F({{x_2},{y_2}})$…(5分)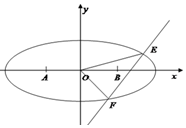
由$\left\{{\begin{array}{l}{y=kx}\\{3{x^2}+4{y^2}=12}\end{array}}\right.$得$x_1^2=\frac{12}{{3+4{k^2}}}$,$y_1^2=\frac{{12{k^2}}}{{3+4{k^2}}}$,同理可得:$x_2^2=\frac{{12{k^2}}}{{3{k^2}+4}}$,$y_2^2=\frac{12}{{3{k^2}+4}}$;
所以${|{OE}|^2}=\frac{{12(1+{k^2})}}{{3+4{k^2}}}$,${|{OF}|^2}=\frac{{12(1+{k^2})}}{{3{k^2}+4}}$
又OE⊥OF,所以$S_{△OEF}^2=\frac{1}{4}{|{OE}|^2}{|{OF}|^2}=36×\frac{{{{({1+{k^2}})}^2}}}{{({3{k^2}+4})({4{k^2}+3})}}$…(8分)
令t=k2+1,则t>1且k2=t-1,所以${S_{△OEF}}^2=36×\frac{{{{({1+{k^2}})}^2}}}{{({3{k^2}+4})({4{k^2}+3})}}=36×\frac{t^2}{{({3t+1})({4t-1})}}$=$-36×\frac{1}{{({\frac{1}{t}+3})({\frac{1}{t}-4})}}=-36×\frac{1}{{{{({\frac{1}{t}-\frac{1}{2}})}^2}-\frac{49}{4}}}$ …(10分)
又$0<\frac{1}{t}<1$,所以$-\frac{49}{4}≤{({\frac{1}{t}-\frac{1}{2}})^2}-\frac{49}{4}<-12$,所以$-\frac{1}{12}<\frac{1}{{{{({\frac{1}{t}-\frac{1}{2}})}^2}-\frac{49}{4}}}≤-\frac{4}{49}$,
所以$\frac{144}{49}≤-36×\frac{1}{{{{({\frac{1}{t}-\frac{1}{2}})}^2}-\frac{49}{4}}}<3$,所以$\frac{12}{7}≤{S_{△OEF}}<\sqrt{3}$,
所以△OEF面积的取值范围为$[{\frac{12}{7},\sqrt{3}})$.…(12分)
点评 本题考查轨迹方程,考查直线与椭圆位置关系的运用,考查三角形面积的计算,考查学生分析解决问题的能力,属于中档题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<m<1 | B. | -4<m<0 | C. | m<1 | D. | -3<m<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 53 | B. | 59 | C. | 66 | D. | 71 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)
如图所示:湖面上甲、乙、丙三艘船沿着同一条直线航行,某一时刻,甲船在最前面的A点处,乙船在中间B点处,丙船在最后面的C点处,且BC:AB=3:1.一架无人机在空中的P点处对它们进行数据测量,在同一时刻测得∠APB=30°,∠BPC=90°.(船只与无人机的大小及其它因素忽略不计)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com