
���� ��1����P��x��y����R��2x��0����Q��0��2y������$\overrightarrow{QT}•\overrightarrow{QR}=0$������E�ķ��̣�
��2�������b��ȡֵ��Χ�������æ�=1+$\frac{1}{4+2b}$��������˵�ȡֵ��Χ��
��� �⣺��1����P��x��y����R��2x��0����Q��0��2y������$\overrightarrow{QT}•\overrightarrow{QR}=0$������E�ķ���Ϊy2=4x��4���֣�
��2����ֱ��L�ķ���Ϊx=my+b����L��Բ���е�m2=2b+b2������I��
��$\left\{{\begin{array}{l}{x=my+b}\\{{y^2}=4x}\end{array}}\right.$��y2-4my-4b=0����=��-4m��2+16b��0����II��
�ɣ�I����II����b�ʣ�-�ޣ�-3���ȣ�0��+�ޣ���8���֣�
��M��x1��y1����N��x2��y2����C��x��y����${y_1}+{y_2}=4m��{x_1}+{x_2}=4{m^2}+2b$��
��$\overrightarrow{OC}$=2��$\overrightarrow{OA}$���ˣ�0������x=�ˣ�x1+x2����y=�ˣ�y1+y2��
����y2=4x�е�${��}^{2}��{y}_{1}+{y}_{2}��^{2}=4�ˣ�{x}_{1}+{x}_{2}��$������=1+$\frac{1}{4+2b}$����$�ˡʣ�\frac{1}{2}��1���ȣ�1��\frac{5}{4}��$12���֣�
���� ���⿼��켣���̣���������֪ʶ�����ã�����ֱ����������λ�ù�ϵ�����ã������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
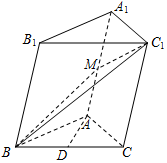 ��б������ABC-A1B1C1�У�AB=AC��ƽ��BB1C1C�͵���ABC����M��D�ֱ����߶�AA1��BC���е㣮
��б������ABC-A1B1C1�У�AB=AC��ƽ��BB1C1C�͵���ABC����M��D�ֱ����߶�AA1��BC���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
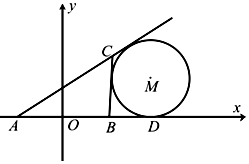 ��ͼ��ʾ���ڡ�ABC�У�AB���е�ΪO����OA=1����D��AB���ӳ����ϣ���$BD=\frac{1}{2}AB$���̶���AB����ƽ�����ƶ�����C��ʹ��ԲM���BC����AC���ӳ������У���ʼ����AB���ӳ��������ڵ�D���Ƕ���C�Ĺ켣Ϊ���ߦ�����AB����ֱ��Ϊx�ᣬOΪ����ԭ����ͼ��ʾ����ƽ��ֱ������ϵ��
��ͼ��ʾ���ڡ�ABC�У�AB���е�ΪO����OA=1����D��AB���ӳ����ϣ���$BD=\frac{1}{2}AB$���̶���AB����ƽ�����ƶ�����C��ʹ��ԲM���BC����AC���ӳ������У���ʼ����AB���ӳ��������ڵ�D���Ƕ���C�Ĺ켣Ϊ���ߦ�����AB����ֱ��Ϊx�ᣬOΪ����ԭ����ͼ��ʾ����ƽ��ֱ������ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ��� | 2012 | 2013 | 2014 | 2015 | 2016 |
| ��ݴ���x | 1 | 2 | 3 | 4 | 5 |
| ������/ʮ��Ԫ | 1 | 6 | 15 | 28 | 45 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | 8 | D�� | 10 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��0�� | B�� | $��-1��-\frac{1}{2}��$ | C�� | $��-2��-\frac{1}{2}��$ | D�� | ��-2��+�ޣ� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com